 por Fabio010 » Sáb Out 22, 2011 13:40
por Fabio010 » Sáb Out 22, 2011 13:40
Já estou à 1 meia hora e tentar resolver o domínio desta função.

Eu tentei assim.
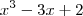
pela regra do ruffini fica
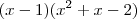
logo

como sabemos

tem de ser maior que zero, logo

x tem de ser diferente de 1.
Dominio =
![x<-2~~~]-1,1[~~~~ ]1, +\infty[ x<-2~~~]-1,1[~~~~ ]1, +\infty[](/latexrender/pictures/beb0a97f029b5b8d35507a8ccfe9b667.png)
Nas soluções a minha solução está errada.
Soluções =
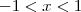
,

-
Fabio010
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por MarceloFantini » Sáb Out 22, 2011 15:41
por MarceloFantini » Sáb Out 22, 2011 15:41
Temos que

. Agora, precisamos que

, logo

. Podemos concluir que

,

e
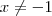
. Portanto, para analisar o sinal disto basta avaliar o sinal de

. Isso acontece quando
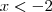
e quando

. A resposta será

.
Eu discordo da solução do gabarito pois se tomar
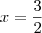
terá
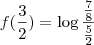
que é solução mas não está no conjunto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio010 » Sáb Out 22, 2011 18:25
por Fabio010 » Sáb Out 22, 2011 18:25
Pois então eu resolvi o problema de forma correcta.
É que as soluções do livro ( B. Demidovitch) estão incorrectas.
Obrigado pela ajuda!!
-
Fabio010
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 21, 2011 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3254 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2890 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1771 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- dominio da funçao
por Thassya » Sex Mai 29, 2009 11:26
- 4 Respostas
- 5171 Exibições
- Última mensagem por Marcampucio

Dom Mai 31, 2009 18:58
Trigonometria
-
- Domínio de uma função
por Jonatan » Qui Jul 29, 2010 15:46
- 0 Respostas
- 1866 Exibições
- Última mensagem por Jonatan

Qui Jul 29, 2010 15:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

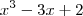 pela regra do ruffini fica
pela regra do ruffini fica 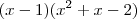

 tem de ser maior que zero, logo
tem de ser maior que zero, logo 
![x<-2~~~]-1,1[~~~~ ]1, +\infty[ x<-2~~~]-1,1[~~~~ ]1, +\infty[](/latexrender/pictures/beb0a97f029b5b8d35507a8ccfe9b667.png)
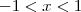 ,
, 


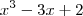 pela regra do ruffini fica
pela regra do ruffini fica 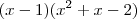

 tem de ser maior que zero, logo
tem de ser maior que zero, logo 
![x<-2~~~]-1,1[~~~~ ]1, +\infty[ x<-2~~~]-1,1[~~~~ ]1, +\infty[](/latexrender/pictures/beb0a97f029b5b8d35507a8ccfe9b667.png)
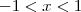 ,
, 

 . Agora, precisamos que
. Agora, precisamos que  , logo
, logo  . Podemos concluir que
. Podemos concluir que  ,
,  e
e 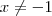 . Portanto, para analisar o sinal disto basta avaliar o sinal de
. Portanto, para analisar o sinal disto basta avaliar o sinal de  . Isso acontece quando
. Isso acontece quando 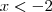 e quando
e quando  . A resposta será
. A resposta será  .
.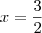 terá
terá 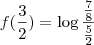 que é solução mas não está no conjunto.
que é solução mas não está no conjunto.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
