Oi para todos. Sou novo aqui, mas em geral eu não sou novo em outro lugar.
O que eu queria saber é o seguinte, suponhamos que temos a derivada dy/dx, e que por uma serie de procedimentos ela venha se tornar, por exemplo, algo como
dh/dsen(xf), ou dy/logx, ou algo parecido.
Como se resolve derivadas deste tipo? isto é, que tenham um diferencial composto, semelhante a uma equação?
O mesmo acontece com as integrais, como resolve-las? Quando o diferencial não é uma simples variavel?



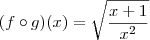
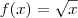 e
e  . Neste caso aplica-se a regra da cadeia (chain rule).
. Neste caso aplica-se a regra da cadeia (chain rule).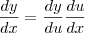
![[f(g(x))]^\prime = f^\prime(g(x))g^\prime(x) [f(g(x))]^\prime = f^\prime(g(x))g^\prime(x)](/latexrender/pictures/43b700ef86b2f826eb9f4de60fe885f5.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)