 por ana tereza » Qui Set 10, 2009 23:47
por ana tereza » Qui Set 10, 2009 23:47
Minha filha está estudando para a prova de amanhã. Na medida do possível tento ajudá-la, no que lembro de matemática, mas empacamos numa questão que ela não prestou atenção na aula e não sabemos qual a lógica do problema. Ela está no 7º ano do Ensino Fundamental.
O problema parece simples, mas não consigo resolver. "A idade de um pai é o quadruplo de seu filho. Dentro de 5 anos, a idade do pai será o triplo da idade do filho. Qual é a idade atual de cada um?" Calculo primero a idade do filho? grata pela ajuda
-
ana tereza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 10, 2009 23:32
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: História
- Andamento: formado
 por Marcampucio » Sex Set 11, 2009 13:41
por Marcampucio » Sex Set 11, 2009 13:41
as idades hoje:
Filho

Pai
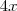
daqui a 5 anos:
Filho

Pai
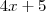
e então a idade do pai será o triplo da do filho:
4x+5=3(x+5)
4x+5=3x+15
4x-3x=15-5
x=10
Hoje o filho tem 10 anos e o pai tem 40 anos, daqui a 5 anos o filho tera 15 e o pai 45, e sua idade será o triplo da do filho.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por ana tereza » Sex Set 11, 2009 15:47
por ana tereza » Sex Set 11, 2009 15:47
Valeu pela ajuda. Nossa, olhando assim dá pra ver que é super fácil. Por que será que cabeça de historiadora não funciona assim... rsss.. Muito obrigada, um abraço.
-
ana tereza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 10, 2009 23:32
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: História
- Andamento: formado
 por gabrielMAT » Qua Out 19, 2011 16:49
por gabrielMAT » Qua Out 19, 2011 16:49
-
gabrielMAT
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Out 19, 2011 15:01
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema envolvendo equação, ajuda !
por LuizCarlos » Qui Jul 28, 2011 15:04
- 1 Respostas
- 1432 Exibições
- Última mensagem por Molina

Sex Jul 29, 2011 16:50
Sistemas de Equações
-
- Como resolvo esse problema envolvendo equação?
por LuizCarlos » Ter Jul 26, 2011 17:15
- 2 Respostas
- 4548 Exibições
- Última mensagem por LuizCarlos

Ter Jul 26, 2011 18:30
Sistemas de Equações
-
- Problema envolvendo função
por marianacarvalhops » Sáb Mai 02, 2009 17:46
- 1 Respostas
- 4412 Exibições
- Última mensagem por Marcampucio

Sáb Mai 02, 2009 18:27
Funções
-
- Problema envolvendo capital
por Crist » Sex Mar 15, 2013 21:57
- 0 Respostas
- 1893 Exibições
- Última mensagem por Crist

Sex Mar 15, 2013 21:57
Equações Diferenciais Ordinárias e Aplicações
-
- Problema envolvendo função
por Carlos28 » Dom Abr 28, 2013 11:15
- 1 Respostas
- 2132 Exibições
- Última mensagem por young_jedi

Dom Abr 28, 2013 20:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



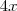

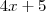


 .
.
 :
: