Provas
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por admin » Qua Jan 23, 2008 13:41
por admin » Qua Jan 23, 2008 13:41
Por ser uma resolução antecipada, estejam a vontade para escreverem comentários e/ou eventuais correções, assim como postarem suas próprias resoluções. Na ocasião do gabarito oficial, faremos uma comparação das respostas.
Questão 1)Um pai tem, hoje, 50 anos e os seus três filhos têm 5, 7 e 10 anos, respectivamente. Daqui a quantos anos a soma das idades dos três filhos será igual à idade do pai?
Resolução)Idéia da situação:
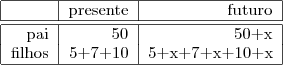
Sendo

o número de anos decorridos.
Queremos que:


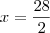

Resposta: daqui a 14 anos.
Conferindo: o pai terá 64 anos, assim como a soma das idades dos filhos (19, 21 e 24).
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Qua Jan 23, 2008 15:53
por admin » Qua Jan 23, 2008 15:53
Questão 2)Durante quanto tempo deve ser aplicado um determinado capital, a juros simples e à taxa de 0,75% ao mês, para que o montante, no final da aplicação, seja igual a

do capital aplicado?
Resolução)Informações:
-juros simples
C: capital inicial
J: total acumulado de juros no período
t: número de meses
i: taxa de juros
M: montante final
t=?
i=0,75% a.m.



Condição do problema:


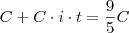
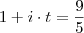
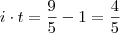
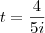
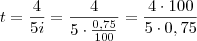
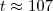
meses
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Qua Jan 23, 2008 21:57
por admin » Qua Jan 23, 2008 21:57
Questão 3)Para que valores de
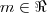
a equação
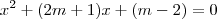
admite raízes reais, distintas e ambas negativas?
Resolução)Condições:
i) raízes reais
ii) raízes distintas
iii) ambas negativas
Através do discriminante, verificamos as condições
i e
ii.
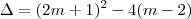


O discriminante em

, representa outra função do segundo grau que não possui raízes reais (possui um par de raízes complexas) e sua parábola é côncava para cima. Ou seja,

é sempre positivo:
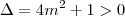
De modo que valerá
i e
ii para todo
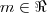
.
Vamos analisar
iii através da soma e do produto das raízes.
Soma:
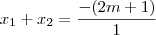
Produto:
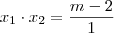
Para que as raízes sejam ambas negativas, a soma deverá ser negativa
e seu produto positivo:
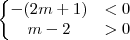
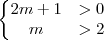
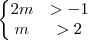
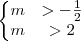
Da intersecção (
e):

sendo
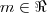
.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Vestibulares
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prova UNIFEI 2008
 por admin » Qua Jan 23, 2008 19:24
por admin » Qua Jan 23, 2008 19:24
- 0 Respostas
- 2842 Exibições
- Última mensagem por admin

Qua Jan 23, 2008 19:24
Vestibulares
-
- [Provas por Indução Matemática] Ajuda, por favor!
por aprendizdematematico » Seg Abr 30, 2012 14:23
- 1 Respostas
- 1763 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 20:56
Estatística
-
- Unifei - prova3 2007
 por WiLLKun » Ter Jan 15, 2008 23:42
por WiLLKun » Ter Jan 15, 2008 23:42
- 10 Respostas
- 15613 Exibições
- Última mensagem por admin

Sáb Abr 05, 2008 17:18
Vestibulares
-
- UNIFEI 2006- Probabilidade
por Luiz C » Qua Jan 13, 2010 23:50
- 2 Respostas
- 3215 Exibições
- Última mensagem por Luiz C

Qui Jan 14, 2010 17:35
Estatística
-
- provas de Introdução à Análise
por ferbonin » Dom Ago 05, 2007 23:08
- 1 Respostas
- 2786 Exibições
- Última mensagem por admin

Ter Ago 28, 2007 03:08
Pedidos de Materiais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


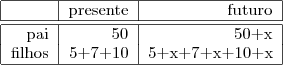
 o número de anos decorridos.
o número de anos decorridos.

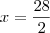


 do capital aplicado?
do capital aplicado?




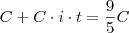
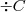
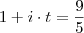
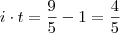
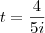
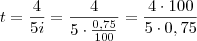
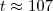 meses
meses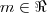 a equação
a equação 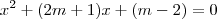 admite raízes reais, distintas e ambas negativas?
admite raízes reais, distintas e ambas negativas?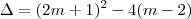


 , representa outra função do segundo grau que não possui raízes reais (possui um par de raízes complexas) e sua parábola é côncava para cima. Ou seja,
, representa outra função do segundo grau que não possui raízes reais (possui um par de raízes complexas) e sua parábola é côncava para cima. Ou seja,  é sempre positivo:
é sempre positivo: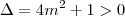
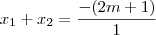
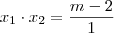
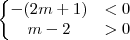
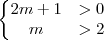
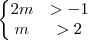
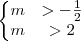
 sendo
sendo 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.