 por bc_anderson » Dom Out 16, 2011 18:03
por bc_anderson » Dom Out 16, 2011 18:03
Boa tarde, meu nome é Anderson, tenho uma dúvida, pois sei que tal problema se resolve por derivada porém não sei como faze-lo.
Um trem deixa uma estação, num certo instante, e vai para a direção norte à razão de 80 km/h. Um segundo trem deixa a estação 2 horas depois e vai na direção leste à razão de 95 km/h. Determine a taxa na qual estão se separando os dois trens 2 horas e 30 minutos depois do segundo trem deixar a estação.
Em relação à minha dúvida, calculei assim:
1º trem: fez e 4h30min a uma veloc. de 80 km/h 360 km. o 2º trem em 2h30mim fez 237 km a uma veloc de 95 km/h. fazendo a diferença encontrei 122,5 km de no período de 2h30min. é isso mesmo?
-
bc_anderson
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 16, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por LuizAquino » Dom Out 16, 2011 18:47
por LuizAquino » Dom Out 16, 2011 18:47
bc_anderson escreveu:Um trem deixa uma estação, num certo instante, e vai para a direção norte à razão de 80 km/h. Um segundo trem deixa a estação 2 horas depois e vai na direção leste à razão de 95 km/h. Determine a taxa na qual estão se separando os dois trens 2 horas e 30 minutos depois do segundo trem deixar a estação.
A figura abaixo ilustra esse exercício.

- estação.png (6.1 KiB) Exibido 3185 vezes
Note que

.
Considerando como tempo inicial o instante no qual o segundo trem deixa a estação, podemos escrever que:


Desse modo, temos que:
![d(t) = \sqrt{[80(t+2)]^2 + (95t)^2} d(t) = \sqrt{[80(t+2)]^2 + (95t)^2}](/latexrender/pictures/3285ad23a5287d390e24a5be63da8ff7.png)
Agora basta calcular
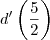
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12552 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10879 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13186 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14792 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5108 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.

![d(t) = \sqrt{[80(t+2)]^2 + (95t)^2} d(t) = \sqrt{[80(t+2)]^2 + (95t)^2}](/latexrender/pictures/3285ad23a5287d390e24a5be63da8ff7.png)
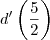 .
.
