 ( limites laterais). Como confirmo se esse numero a, é a assintota vertical?
( limites laterais). Como confirmo se esse numero a, é a assintota vertical?Se por exemplo o
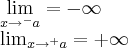
( limites laterias nao coincidem...)
A assintota existe?

 ( limites laterais). Como confirmo se esse numero a, é a assintota vertical?
( limites laterais). Como confirmo se esse numero a, é a assintota vertical?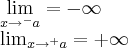

isanobile escreveu:O "candidato" a assintota vertical, é aquele numero (a) que zera o denominador certo?
isanobile escreveu:Tenho que fazer entãoe
( limites laterais).
isanobile escreveu:Como confirmo se esse numero a, é a assintota vertical?


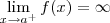
isanobile escreveu:Se por exemplo oe
( limites laterias nao coincidem...)
A assintota existe?
 .
.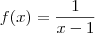 .
.

 (já que os limites laterais são distintos), mas a reta x = 1 existe e representa uma assíntota vertical do gráfico de f. Veja a figura abaixo.
(já que os limites laterais são distintos), mas a reta x = 1 existe e representa uma assíntota vertical do gráfico de f. Veja a figura abaixo.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
