 por esquilowww » Sex Out 14, 2011 23:34
por esquilowww » Sex Out 14, 2011 23:34
Olá pessoal, gostaria de saber como procedo com esta questão, pois me disseram que eu deveria derivá-la e igualar a 0. Porém quando o faço, "travo" e não consigo mais fazer. Gostaria de uma ajuda de como devo proceder para resolver esta questão.
Considere a função f definida por  . Sabe-se que esta função tem um ponto de máximo no ponto de abscissa 1 e um ponto de mínimo no ponto de abscissa -1. Uma de suas raizes é zero e não tem outras raízes reais. Determine os valores de a, b e c.
. Sabe-se que esta função tem um ponto de máximo no ponto de abscissa 1 e um ponto de mínimo no ponto de abscissa -1. Uma de suas raizes é zero e não tem outras raízes reais. Determine os valores de a, b e c.Além desta também tem outra questão que estou "quebrando cabeça" e não sei nem por onde começar. Segue.
A Receita mensal de vendas de um produto, em uma empresa, e seu custo total são representados pelas funções 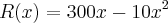 e
e 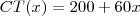 , onde a variável x representa as quantidades produzidas e vendidas:
, onde a variável x representa as quantidades produzidas e vendidas:
a) Obtenha a quantidade que maximiza o Lucro.
b) Mostre que, para o resultado obtido no ítem “a”, o custo marginal é igual a receita marginal.Desde já agradeço.
-
esquilowww
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 14, 2011 23:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração/Ciências Contábeis
- Andamento: cursando
 por LuizAquino » Sáb Out 15, 2011 08:20
por LuizAquino » Sáb Out 15, 2011 08:20
Exercício 1(...) Sabe-se que esta função tem um ponto de máximo no ponto de abscissa 1 e um ponto de mínimo no ponto de abscissa -1. (...)
Isso significa que
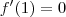
e

.
(...) Uma de suas raizes é zero (...)
Isso significa que

.
(...) e não tem outras raízes reais (...)
Isso significa que as outras duas raízes são números complexos.
Resumindo o problema, usando as informações você pode montar o seguinte sistema:
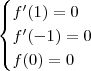
Agora termine a resolução.
Exercício 2a) Obtenha a quantidade que maximiza o Lucro.
Já que
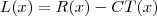
, deve ocorrer que

.
O lucro máximo ocorre no ponto
c tal que
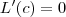
e
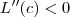
.
b) Mostre que, para o resultado obtido no ítem “a”, o custo marginal é igual a receita marginal.
Isto é, deve-se verificar que

.
Agora termine a resolução.
ObservaçãoEu recomendo que você assista a vídeo-aula "21. Cálculo I - Teste da Primeira e da Segunda Derivada". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por esquilowww » Sáb Out 15, 2011 17:20
por esquilowww » Sáb Out 15, 2011 17:20
LuizAquino escreveu:Exercício 1(...) Sabe-se que esta função tem um ponto de máximo no ponto de abscissa 1 e um ponto de mínimo no ponto de abscissa -1. (...)
Isso significa que
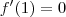
e

.
(...) Uma de suas raizes é zero (...)
Isso significa que

.
(...) e não tem outras raízes reais (...)
Isso significa que as outras duas raízes são números complexos.
Resumindo o problema, usando as informações você pode montar o seguinte sistema:
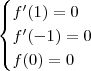
Agora termine a resolução.
Exercício 2a) Obtenha a quantidade que maximiza o Lucro.
Já que
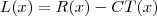
, deve ocorrer que

.
O lucro máximo ocorre no ponto
c tal que
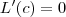
e
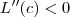
.
b) Mostre que, para o resultado obtido no ítem “a”, o custo marginal é igual a receita marginal.
Isto é, deve-se verificar que

.
Agora termine a resolução.
ObservaçãoEu recomendo que você assista a vídeo-aula "21. Cálculo I - Teste da Primeira e da Segunda Derivada". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
Luiz, antes de tudo gostaria de lhe agradecer pelas informações, pois consegui resolver os 2 problemas, só queria saber se fiz corretamente... rs.
1ª questão:
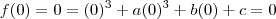
ENTÂO:

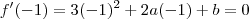 LOGO: 3 -2a + b = 0
LOGO: 3 -2a + b = 0 LOGO: 3 + 2a + b = 0
LOGO: 3 + 2a + b = 0Com base nas informações obtemos o sitema.

Resolvendo o sitema obtemos o resultado que
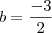
Utilizando o resultado de

Utilizaremos em uma das equações do sistema.
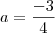
Agora a 2ª questão:
letra a)
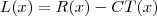

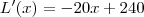

Como o lucro máximo se dá onde

e
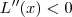
Temos:


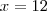
A quantidade que maximiza o lucro será de 12 unidades.
letra b)
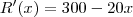
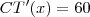
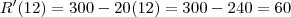
Ai estão as minhas respostas, gostaria de saber se as acertei.
Mais uma vez torno a lhe agradecer Luiz.
Um abraço.
-
esquilowww
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 14, 2011 23:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração/Ciências Contábeis
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar a e b
por gabrielloren » Qua Set 05, 2012 16:12
- 1 Respostas
- 1987 Exibições
- Última mensagem por Russman

Qua Set 05, 2012 18:59
Números Complexos
-
- Determinar p
por Rafael16 » Sex Dez 28, 2012 17:50
- 3 Respostas
- 2131 Exibições
- Última mensagem por e8group

Sáb Dez 29, 2012 17:09
Conjuntos
-
- Determinar x1, x2 e x3
por nanasouza123 » Sex Set 22, 2017 20:50
- 0 Respostas
- 2031 Exibições
- Última mensagem por nanasouza123

Sex Set 22, 2017 20:50
Polinômios
-
- Determinar o domínio
por rodsales » Qui Jun 18, 2009 20:59
- 2 Respostas
- 3761 Exibições
- Última mensagem por rodsales

Sex Jun 19, 2009 20:58
Trigonometria
-
- Determinar a função
por yonara » Ter Jun 30, 2009 20:19
- 1 Respostas
- 3711 Exibições
- Última mensagem por Felipe Schucman

Seg Ago 03, 2009 21:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Sabe-se que esta função tem um ponto de máximo no ponto de abscissa 1 e um ponto de mínimo no ponto de abscissa -1. Uma de suas raizes é zero e não tem outras raízes reais. Determine os valores de a, b e c.
. Sabe-se que esta função tem um ponto de máximo no ponto de abscissa 1 e um ponto de mínimo no ponto de abscissa -1. Uma de suas raizes é zero e não tem outras raízes reais. Determine os valores de a, b e c.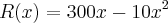 e
e 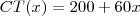 , onde a variável x representa as quantidades produzidas e vendidas:
, onde a variável x representa as quantidades produzidas e vendidas:

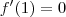 e
e  .
. .
.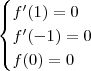
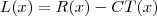 , deve ocorrer que
, deve ocorrer que  .
.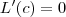 e
e 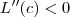 .
. .
.
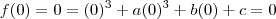 ENTÂO:
ENTÂO: 
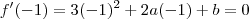


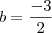
 Utilizaremos em uma das equações do sistema.
Utilizaremos em uma das equações do sistema.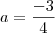

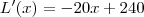


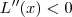


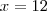
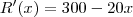
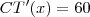
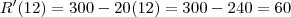
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
