 por wadson leite » Qua Out 12, 2011 15:53
por wadson leite » Qua Out 12, 2011 15:53
estava estudando para minha prova de calculo nesta sexta e estou com dúvidas que acho que podem ser básicas, ou não...
por isso estou aqui postando minhas duas dúvidas por enquanto:
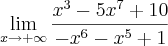
![\lim_{x\rightarrow +\infty}\frac{\sqrt[2]{x^2+1}}{3x+2} \lim_{x\rightarrow +\infty}\frac{\sqrt[2]{x^2+1}}{3x+2}](/latexrender/pictures/7f7eee5372d8be1135c5f6736c82138d.png)
bom no primeiro caso eu comecei tentando divisão de polinômios, mas me enrolei..
aí tentei dividir o numerado e o denominador pelo fator de maior grau, no caso x^7; só que aí no denominador ficaria 0, já que todos os fatores iriam tender a 0;
briot rufini eu nem tentei e não sei nem como começar a fatorar esse negócio...
no segundo caso, tentei usar o conjugado, mas não cheguei em lugar nenhum e multiplicar por um fator igual a 1 tbm não deu em nada..
não sei o que fazer..
se eu conseguir entender esses dois casos, já é metade do caminho andado pra eu entender a lista que tenho que resolver..
obrigado
-
wadson leite
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 31, 2009 16:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em fisica
- Andamento: cursando
 por joaofonseca » Qua Out 12, 2011 20:29
por joaofonseca » Qua Out 12, 2011 20:29
Intuitivamente digo-te que o primeiro exemplo tende para

.Basta observar que o grau do numerado é maior que o grau do denominador. Se o sinal negativo dos coeficientes de maior grau atrapalham, experimenta tira-los para fora, alterando os sinais dos restantes termos.
No segundo caso é necessário fazer uma nota prévia.Todos sabemos que

e que se

então podemo-nos limitar à parte positiva de

, ou seja
x.
Então:
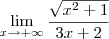
Agora dividimos o numerador por

e o denominador por
x, pelas razões que indiquei antes.
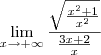
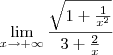


-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por wadson leite » Qua Out 12, 2011 22:25
por wadson leite » Qua Out 12, 2011 22:25
sim entendo que o numerador é de grau maior que o denominador, e entendo que tende a infinito, mas qual é o limite?
lembrando que não posso usar l'hospital e nem tabela.
eu acredito que tenha alguma forma de dividir o numerado pelo denominador ou então simplificar a expressão. e quanto ao segundo caso, muito obrigado pela resposta...
entendi onde eu estava errando..
-
wadson leite
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 31, 2009 16:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em fisica
- Andamento: cursando
 por LuizAquino » Qua Out 12, 2011 22:42
por LuizAquino » Qua Out 12, 2011 22:42
wadson leite escreveu:sim entendo que o numerador é de grau maior que o denominador, e entendo que tende a infinito, mas qual é o limite?
Note que:

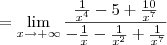
Quando
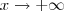
, temos que o numerador dessa fração tende para -5, enquanto que o denominador tende para 0 (porém se aproximando por valores negativos). Desse modo, o resultado final será:
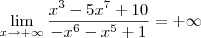
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por wadson leite » Qua Out 12, 2011 23:39
por wadson leite » Qua Out 12, 2011 23:39
obrigado.. agora entendi..
-
wadson leite
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 31, 2009 16:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em fisica
- Andamento: cursando
 por wadson leite » Qui Out 13, 2011 09:54
por wadson leite » Qui Out 13, 2011 09:54
joaofonseca escreveu:No segundo caso é necessário fazer uma nota prévia.Todos sabemos que

e que se

então podemo-nos limitar à parte positiva de

, ou seja
x.
Então:
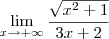
Agora dividimos o numerador por

e o denominador por
x, pelas razões que indiquei antes.
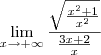
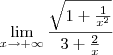


tá e se eu colocar tendendo a menos infinito posso usar a mesma analogia:
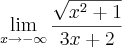
e dividir o numerador por

e o denominador por -x
fazendo a equação ficar dessa forma:
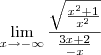
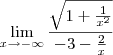


estaria certo?
-
wadson leite
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 31, 2009 16:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em fisica
- Andamento: cursando
 por wadson leite » Sex Out 14, 2011 16:39
por wadson leite » Sex Out 14, 2011 16:39
ninguém???
-
wadson leite
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 31, 2009 16:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em fisica
- Andamento: cursando
 por joaofonseca » Sex Out 21, 2011 10:35
por joaofonseca » Sex Out 21, 2011 10:35
Fazendo a mesma analogia, claro.
Repara que a função modulo/valor absoluto, pode ser defenida por ramos da seguinte forma:
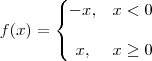
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por wadson leite » Sex Out 21, 2011 11:28
por wadson leite » Sex Out 21, 2011 11:28
obrigado, joão
-
wadson leite
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 31, 2009 16:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em fisica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4751 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4775 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4803 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2787 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
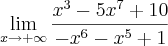
![\lim_{x\rightarrow +\infty}\frac{\sqrt[2]{x^2+1}}{3x+2} \lim_{x\rightarrow +\infty}\frac{\sqrt[2]{x^2+1}}{3x+2}](/latexrender/pictures/7f7eee5372d8be1135c5f6736c82138d.png)


 .Basta observar que o grau do numerado é maior que o grau do denominador. Se o sinal negativo dos coeficientes de maior grau atrapalham, experimenta tira-los para fora, alterando os sinais dos restantes termos.
.Basta observar que o grau do numerado é maior que o grau do denominador. Se o sinal negativo dos coeficientes de maior grau atrapalham, experimenta tira-los para fora, alterando os sinais dos restantes termos. e que se
e que se  então podemo-nos limitar à parte positiva de
então podemo-nos limitar à parte positiva de  , ou seja
, ou seja 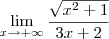
 e o denominador por
e o denominador por 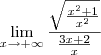
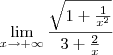




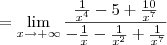
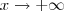 , temos que o numerador dessa fração tende para -5, enquanto que o denominador tende para 0 (porém se aproximando por valores negativos). Desse modo, o resultado final será:
, temos que o numerador dessa fração tende para -5, enquanto que o denominador tende para 0 (porém se aproximando por valores negativos). Desse modo, o resultado final será: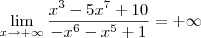

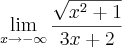
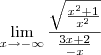
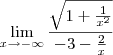

 estaria certo?
estaria certo?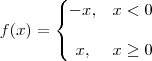
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
