Campeão, eu achei 10 cm como raio... Tem o gabarito para ver se acertei ?
Fiz o seguinte, se você reparar existe um triângulo ACD retângulo em A, pois como CD é o diâmetro do círculo então o ângulo  tem 90º. Logo, usando a
relação do triângulo que diz que o quadrado da altura é igual ao produto dos lados, temos:
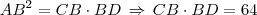
Mas o problema nos diz que a diferença entre CB e BD é de 12 cm, logo temos:
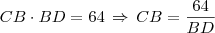

Substituindo CB na segunda equação temos:
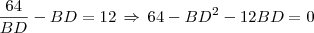
Cujas as raízes são: -16 e 4. Como estamos lidando com medidas métricas, logo -16 não nos serve, sobrando apenas BD = 4 cm, o que nos dá um CB = 16 cm, somando CB e BD para achar o diâmetro temos CB + BD = 20 cm => raio = 10 cm.
Se cometi algum erro, me perdoe...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
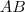 de 8cm é perpendicular ao diâmetro
de 8cm é perpendicular ao diâmetro  de uma circonferência, tendo suas extremidades no diâmetro e na circunferência. O diâmetro fica, então, separado em dois segmentos cuja diferença entre eles é de 12 cm. Dessa forma, a medida do raio da circonferência é:
de uma circonferência, tendo suas extremidades no diâmetro e na circunferência. O diâmetro fica, então, separado em dois segmentos cuja diferença entre eles é de 12 cm. Dessa forma, a medida do raio da circonferência é:

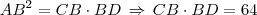
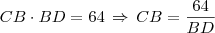

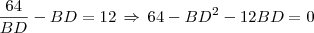

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.