Grande mestre Fernando, tudo em paz ??
Temos três círculos tangentes entre si, cada um tem um raio de 10 cm, se ligarmos os centro de cada um através do ponto tangente entre eles teremos um triângulo equilátero de lado 20 cm e temos uma parte da figura sombreada dentro do triângulo.
A área do triângulo equilátero é

, então fica igual a

segundo os dados dado no problema. Agora temos que tirar a área do setor circular (pois ao subtrair a área de cada setor circular, são 3 no total, da área do triângulo equilátero teremos a
área da figura entre os círculos), como sabemos que os ângulos internos de um triângulo equilátero são 60º, logo vamos calcular a área do setor circular usando graus, veja:

Agora, multipliquemos esse valor por 3 (pois são três círculos) e subtraímos da área do triângulo, teremos:
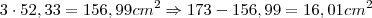
Agora, basta somar os 16,01 cm^2 da área sombreada com a área do círculo inferior, que é de 314 cm^2, logo você terá 330,01 cm^2, aproximadamente 330 cm^2.
Espero ter feito tudo certo e ajudado...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...



 , então fica igual a
, então fica igual a  segundo os dados dado no problema. Agora temos que tirar a área do setor circular (pois ao subtrair a área de cada setor circular, são 3 no total, da área do triângulo equilátero teremos a
segundo os dados dado no problema. Agora temos que tirar a área do setor circular (pois ao subtrair a área de cada setor circular, são 3 no total, da área do triângulo equilátero teremos a 
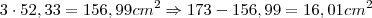
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)