Ola queria saber um bom programa para iniciantes para fazer graficos de funçoes ou graficos de algumas somas parciais de uma série. Na internet tem varias opções mas queria uma indicação de alguem que ja usou ou conhece algum bom.
Flávio Santana



380625 escreveu:Ola queria saber um bom programa para iniciantes para fazer graficos de funçoes ou graficos de algumas somas parciais de uma série.



380625 escreveu:Ola gostei muito do seu canal no youtube sobre o Geogebra.

380625 escreveu:Quero mostrar atravez do programa o fenômeno de Gibbs, porem não consigo expressar no programa a sequencia das somas parcias da função abaixo
f(x) = Soma[Sequência[(2/pi)*(1 - ((-1)^n)*sin(n*x))/n, n, 1, 5]]
f(x) = Soma[Sequência[(2/pi)*(1 - ((-1)^n)*sin(n*x))/n, n, 1, k]]


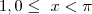 .
.
380625 escreveu:Eu tenho essa função
Calculando a Série de Fourier chegamos em f(x) (aquela que te mandei no outro email).
380625 escreveu:O que quero fazer é mostrar que as somas parcias de f(x) (dado no outro email) se aproxima dessa função cada vez que somo n termos.
No programa da a função perfeitamente mas não consigo mostrar que cada soma parcial de f(x) (outro email )se aproxima dessa f(x).

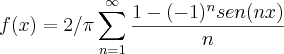 , eu conferi e olhei no livro poi este é um exemplo do Zill pagina 215.
, eu conferi e olhei no livro poi este é um exemplo do Zill pagina 215.
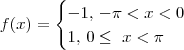 tem o formato:
tem o formato:![f(x) = \frac{2}{\pi} \sum_{n = 1}^{\infty} \frac{[1 - (-1)^n]\,\textrm{sen}\,(nx)}{n} f(x) = \frac{2}{\pi} \sum_{n = 1}^{\infty} \frac{[1 - (-1)^n]\,\textrm{sen}\,(nx)}{n}](/latexrender/pictures/aa93932448fdf307ac5b2dd76dbce2aa.png)
380625 escreveu:

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes