Provas
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por WiLLKun » Ter Jan 15, 2008 23:42
por WiLLKun » Ter Jan 15, 2008 23:42
Olá gente
vou fazer o vestibular da unifei este final de semana, e qdo fui dar uma conferida na prova dissertativa de matematica, fornecida por eles, mal conseguia responder as questoes e mto menos entender as respostas dadas por eles, ou conseguir seguir a linha de raciocinio para chegar nestes resultados, gostaria de saber se ninguen poderia fazer as resoluçoes dessa prova, sao 10 questoes
http://www.vestibular.unifei.edu.br/arquivos_upload/provas/2007/Prova%203%20-%202007%20-%20Matematica.docse tiver como fazer essas resoluçoes de modo q seja possivel compreender
obrigado ^^
-
WiLLKun
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jan 15, 2008 23:23
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sáb Jan 19, 2008 04:36
por admin » Sáb Jan 19, 2008 04:36
Olá WiLLKun!
Nesta semana, eu particularmente não tenho disponibilidade de tentar resolver estas 10 questões no prazo que você precisa.
Como por enquanto ninguém respondeu, caso você tenha alguma dúvida mais específica, talvez possamos ajudar.
Uma resolução de prova inteira, da forma didática como você espera, demanda mais tempo e dedicação de quem for ajudar, o que entra em conflito com sua expectativa para este final de semana.
Sendo assim, durante estes seus estudos às vésperas, acredito que as dúvidas mais pontuais ainda poderão ser respondidas.
De qualquer forma, posteriormente, dedicarei tempo para cada uma das questões e postarei aqui meus comentários.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Sáb Jan 19, 2008 06:24
por admin » Sáb Jan 19, 2008 06:24
Resolução da questão 1:
unifei_prova3_2007_questao1.PDF
Apenas anexando a prova, no caso do link original não funcionar para os próximos leitores:
UNIFEI - Prova 3 - 2007 - Matematica.doc
Você não está autorizado a ver ou baixar esse anexo.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Sáb Jan 19, 2008 07:39
por admin » Sáb Jan 19, 2008 07:39
Resolução da questão 2:
unifei_prova3_2007_questao2.PDF
Você não está autorizado a ver ou baixar esse anexo.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Sáb Jan 19, 2008 18:03
por admin » Sáb Jan 19, 2008 18:03
Resolução da questão 3:
unifei_prova3_2007_questao3.PDF
Você não está autorizado a ver ou baixar esse anexo.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por WiLLKun » Sáb Jan 19, 2008 21:24
por WiLLKun » Sáb Jan 19, 2008 21:24
nossa cra valeu heim... sei lah tem materias q nao peguei mto bem na escola pq tive de mudar de colegio... log e funçao mais avançado tenhu dificuldade ainda
como estasprovas soh vem com resultado fikei boiando em algumas e outras tive duvida por nao encontrar o mesmo resultado
tuas resoluçoes esto boas ^^ vlww mesmo... amanhan eh minha prova pratica de mat e fisica, mas fazer oq neh, as vezes eh ateh bom eu nao passar dessa vez, passar no vestibular nao qr dizer q vai se dar bem na facul, nunk fis cursinho tmb
vlwww por tudo e se tver como vc terminar de fazer a prova... soh nao precisa ter pressa
-
WiLLKun
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jan 15, 2008 23:23
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Dom Jan 20, 2008 19:29
por admin » Dom Jan 20, 2008 19:29
Olá
WiLLKun.
Espero que você tenha ido bem na prova!
Estou tentando fazer as resoluções de forma compreensível.
Mas ressalto que novos questionamentos sempre podem ser feitos.
Quanto mais soubermos especificar nossas dúvidas, melhor.
Nas resoluções de problemas sempre são utilizados resultados previamente obtidos: teoremas, propriedades, fórmulas etc.
Caso algum trecho tenha ficado obscuro, compartilhe conosco.
Resolução da questão 4:
unifei_prova3_2007_questao4.PDF
Você não está autorizado a ver ou baixar esse anexo.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Ter Jan 22, 2008 18:50
por admin » Ter Jan 22, 2008 18:50
Diferentemente das outras respostas do gabarito, neste caso, a resolução tem que ser completa.
Entretanto, considerando as entre-linhas, ainda podemos questionar:
i) 1o. membro?
 ii)
ii)Soma das raízes?
 iii)
iii)Produto das raízes?
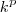
Nesta resolução, vamos evidenciar estes passos, pois provavelmente são os principais causadores de dúvidas.
Començado pelo 1o. membro, vamos reescrevê-lo em etapas para entendermos o que está no gabarito:
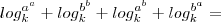





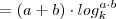
Então, o passo
(i) está mais detalhado.
Onde
a e
b são, por hipótese, as raízes da equação:

Agora, vamos percorrer a obtenção da soma e do produto das raízes de uma equação do segundo grau, para entendermos
(ii) e
(iii).
Vamos considerar esta equação, onde

,

.
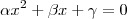
Onde as duas raízes são:
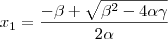
e
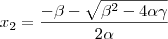
Soma das raízes:

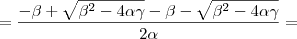
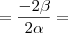

Voltando para a equação do problema:

Temos que:

e

Logo,
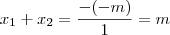
E como
a e
b são as raízes,

(passo
ii)
Produto das raízes:

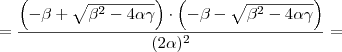

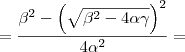
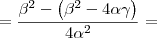
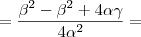

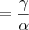
Novamente, voltando para a equação do problema:

Temos que:

,

e
a,
b são raízes.
Logo,
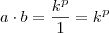
(passo
iii)
Portanto, percorremos as entre-linhas do gabarito, pois uma das maneiras para resolvermos um exercício algébrico do tipo "mostre que", é partirmos exclusivamene de um membro da equação e chegarmos ao outro, provando que são de fato iguais.
Eis um resumo do que fizemos:
Partindo do 1o. membro:
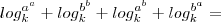

Considerando a equação:

Vimos que a soma das raízes é:

Produto das raízes:

Agora, substituíremos estes resultados na continuação do desenvolvimento do 1o. membro.
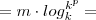

(que é o 2o. membro, onde queríamos chegar)
É claro que na prática, ou em uma resolução pessoal, nós podemos (ou, vocês podem) fazer em 4 linhas, como no gabarito.
Mas, a intenção aqui foi detalhar um pouco.
Reparem que os questionamentos podem não ter fim, como por exemplo:
-Como obtemos aquelas raízes de uma equação de segundo grau?
-Como chegamos à "fórmula de Bhaskara"?
-E as propriedades usadas de log?
-E este trecho?

Vemos que em toda resolução ficam implícitos conhecimentos prévios.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Sáb Abr 05, 2008 17:18
por admin » Sáb Abr 05, 2008 17:18
1º passo) encontrar a medida dos lados
Como formam uma P.A., temos:



Então, as medidas são 5, 8 e 11.
2º passo) testar se o triângulo é retângulo, através do teorema de Pitágoras
Pois como queremos os cossenos dos ângulos internos, a obtenção seria mais simples, fazendo cateto adjacente sobre hipotenusa.
Mas ao testar constatamos que não vale o teorema de Pitágoras para estas medidas, ou seja, o triângulo
não é retângulo.

3º passo) aplicar o teorema dos cossenos para cada ângulo

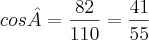

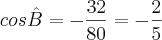


4º passo) calcular a soma
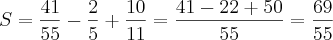
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Vestibulares
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prova UNIFEI 2008
 por admin » Qua Jan 23, 2008 19:24
por admin » Qua Jan 23, 2008 19:24
- 0 Respostas
- 2841 Exibições
- Última mensagem por admin

Qua Jan 23, 2008 19:24
Vestibulares
-
- UNIFEI 2006- Probabilidade
por Luiz C » Qua Jan 13, 2010 23:50
- 2 Respostas
- 3215 Exibições
- Última mensagem por Luiz C

Qui Jan 14, 2010 17:35
Estatística
-
- Provas de Matematica UNIFEI 2008
por WiLLKun » Qua Jan 23, 2008 01:21
- 3 Respostas
- 10119 Exibições
- Última mensagem por admin

Qua Jan 23, 2008 21:57
Vestibulares
-
- Newsletter #1 - 04/09/2007
por admin » Ter Dez 11, 2007 18:08
- 0 Respostas
- 4872 Exibições
- Última mensagem por admin

Ter Dez 11, 2007 18:08
Informações Gerais
-
- Newsletter #2 - 28/09/2007
por admin » Ter Dez 11, 2007 19:11
- 1 Respostas
- 5454 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 19:43
Informações Gerais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





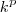
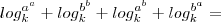





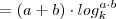

 ,
,  .
.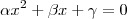
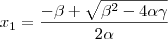
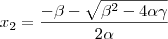

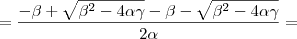
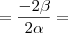

 e
e 
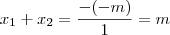
 (passo
(passo 
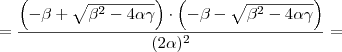

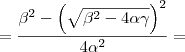
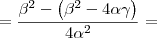
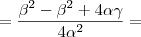

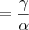
 e
e 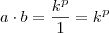 (passo
(passo 

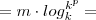

 (que é o 2o. membro, onde queríamos chegar)
(que é o 2o. membro, onde queríamos chegar)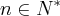 :
: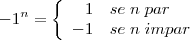
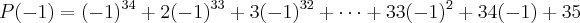



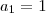 :
:

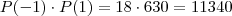





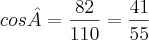

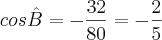


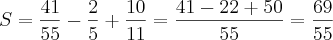


 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
