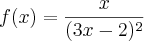 , a reta tangente ao gráfico de f no ponto (a,f(a)) é horizontal quando "a" vale quanto?
, a reta tangente ao gráfico de f no ponto (a,f(a)) é horizontal quando "a" vale quanto?Eu pensei assim:
Y-Yo = Y'(Xo)(X - Xo)
Como a reta é horizontal, o coeficiente angular =derivada= Y'(Xo) é zero, assim
Y-f(a) = 0(X -Xo)
Y=f (a)
Y=
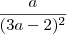
mas travei...


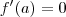 ?
?
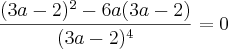
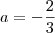 .
.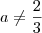 , então podemos escrever que:
, então podemos escrever que: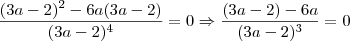
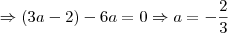
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)