 por Claudin » Dom Set 25, 2011 17:35
por Claudin » Dom Set 25, 2011 17:35
Como analisar se uma função é derivável ou não?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Set 25, 2011 23:15
por LuizAquino » Dom Set 25, 2011 23:15
Claudin escreveu:Como analisar se uma função é derivável ou não?
Dado uma função f e um ponto c em seu domínio, para analisar se f é derivável em c, então basta analisar se o limite abaixo existe e é finito:
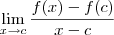
Vale destacar que dizemos que f é derivável em um intervalo (a, b) de seu domínio, se f é derivável em cada ponto desse intervalo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Set 29, 2011 21:41
por Claudin » Qui Set 29, 2011 21:41
Não compreendi.
Mas o denominador no caso não seria uma indeterminação?
Por exemplo a função a seguir é derivável em x=1?
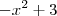
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Out 01, 2011 09:45
por LuizAquino » Sáb Out 01, 2011 09:45
Claudin escreveu:Por exemplo a função a seguir é derivável em x=1?
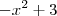
Aplicando o que eu disse anteriormente, para verificar se a função
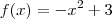
é derivável em x = 1, você tem que analisar o limite abaixo:
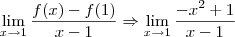
Você precisa então responder a seguinte pergunta: esse limite existe e é finito?
ObservaçãoVale lembrar que dizemos que
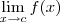
existe quando temos que
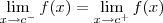
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- A função é derivável
por Ana Maria da Silva » Qua Jun 12, 2013 20:51
- 1 Respostas
- 1181 Exibições
- Última mensagem por e8group

Sex Jun 14, 2013 20:41
Cálculo: Limites, Derivadas e Integrais
-
- Função derivável no ponto
por Lilica » Qua Jun 29, 2011 16:02
- 3 Respostas
- 3303 Exibições
- Última mensagem por LuizAquino

Qua Jun 29, 2011 17:04
Cálculo: Limites, Derivadas e Integrais
-
- Seja ?(x) uma função derivavel
por kak9 » Ter Out 02, 2018 15:33
- 0 Respostas
- 2977 Exibições
- Última mensagem por kak9

Ter Out 02, 2018 15:33
Cálculo: Limites, Derivadas e Integrais
-
- dúvida sobre função derivável
por MariPC » Sáb Ago 15, 2009 14:45
- 6 Respostas
- 6323 Exibições
- Última mensagem por MarceloFantini

Sex Jun 03, 2011 16:02
Cálculo: Limites, Derivadas e Integrais
-
- analise
 por leticiapires52 » Sex Abr 17, 2015 12:36
por leticiapires52 » Sex Abr 17, 2015 12:36
- 1 Respostas
- 2626 Exibições
- Última mensagem por rzarour

Ter Mar 01, 2016 00:00
Óptica
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



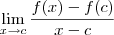

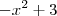

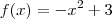 é derivável em x = 1, você tem que analisar o limite abaixo:
é derivável em x = 1, você tem que analisar o limite abaixo: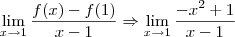
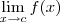 existe quando temos que
existe quando temos que 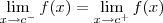 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.