 por Allanx » Sáb Set 24, 2011 15:30
por Allanx » Sáb Set 24, 2011 15:30
Olá pessoal estava estudando log e me deparei com exercícios onde fiquei completamente perdido, não vou negar, são muitos. Porém, postarei apenas os primeiros de cada sequência, se não for o bastante para resolver os outros eu volto a postar( o correto seria criar um novo tópico, certo?)
1) Simplificar

Essa eu não tive e idéia nem por onde começar, pensei em tentar mudar de base, mas não deu certo... praticamente não saí do zero. Log dentro de log é uma coisa muito estranha para mim, existe alguma regra prática para esse tipo de situação?
Resposta:

Consegui resolver a primeira, era bobeira, elevei 10 a log a ( já que estava dividindo)
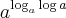
podendo assim simplificar para

2) Se

e
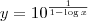
prove que:
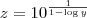
Como cada uma das definições depende da outra eu fiquei perdido ao tentar unificá-las, sem sucesso também. Como faço para isolar uma incógnita em uma situação dessas?
3) Resolver a equação

Utilizando as propriedades e transformando tudo em log ficou assim:
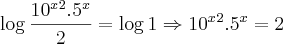
Resposta: -1 e log 2
Por enquanto são só essas, tentando refazer meus passos acabei conseguindo algumas que não havia conseguido antes.
Obrigado pela atenção
-
Allanx
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mar 25, 2011 23:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sáb Set 24, 2011 17:07
por LuizAquino » Sáb Set 24, 2011 17:07
Allanx escreveu:o correto seria criar um novo tópico, certo?
Sim, por questão de organização. Inclusive, o ideal é que em cada tópico haja apenas um exercício.
Allanx escreveu:1) Simplificar

Note que aplicando mudança de base, podemos dizer que:

Lembrando-se da propriedade
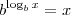
, temos que:

Allanx escreveu:2) Se

e
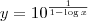
prove que:
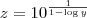
Aplicando a definição de logaritmo, podemos escrever que:
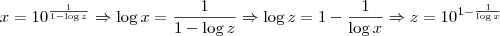

Agora basta substituir x na expressão para z.
Allanx escreveu:3) Resolver a equação

Isso é simplesmente uma equação polinomial do 2° grau. Resolva normalmente calculando o discriminante.

Lembrando-se que

, temos que:

Agora basta você calcular as duas soluções usando

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas de logarítmos
por Danilo Dias Vilela » Qua Ago 18, 2010 16:22
- 4 Respostas
- 2678 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Ago 20, 2010 19:36
Logaritmos
-
- sistemas de equãções
por Rejane Sampaio » Sex Set 12, 2008 23:54
- 1 Respostas
- 2662 Exibições
- Última mensagem por admin

Ter Set 16, 2008 20:31
Estatística
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 17:34
- 1 Respostas
- 1273 Exibições
- Última mensagem por Molina

Qua Set 09, 2009 17:54
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 21:19
- 1 Respostas
- 1433 Exibições
- Última mensagem por Elcioschin

Qua Set 09, 2009 22:27
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 23:55
- 1 Respostas
- 2298 Exibições
- Última mensagem por Molina

Qui Set 10, 2009 14:15
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


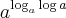 podendo assim simplificar para
podendo assim simplificar para 
 e
e 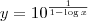 prove que:
prove que: 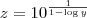

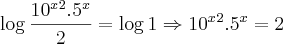



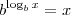 , temos que:
, temos que:
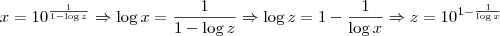



 , temos que:
, temos que:
 .
.





