 por beel » Qua Set 21, 2011 13:09
por beel » Qua Set 21, 2011 13:09
Qual a derivada f'(a) de sen(2x), sendo sen (2x) = 2sen(x).cos(x)?
Meu raciocínio foi:
f'(a) = (2sen(x))'.cos(x) + (2sen(x)).(cos(x))' =
2(cos(x)).cos(x) + 2.sen(x)(-sen (x))
2cos(x)² - 2sen(x)²
ta correto?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Qua Set 21, 2011 15:11
por Neperiano » Qua Set 21, 2011 15:11
Ola
A derivada fica assim
2cosx.cosx + 2senx.-senx
2cosx^2 -2senx^2
Está correto sim
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Qua Set 21, 2011 16:51
por LuizAquino » Qua Set 21, 2011 16:51
isanobile escreveu:2cos(x)² - 2sen(x)²
Neperiano escreveu:2cosx^2 -2senx^2
O correto é escrever:

Podemos ainda simplificar a resposta aplicando a identidade trigonométrica

. Desse modo, podemos reescrever o resultado como:
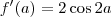 Observação
ObservaçãoCuidado para não confundir

com

e nem

com
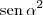
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Out 16, 2011 17:07
por beel » Dom Out 16, 2011 17:07
Ok,obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4791 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4437 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
-
- Derivada funções trigonométricas
por samysoares » Seg Mar 04, 2013 13:38
- 4 Respostas
- 2601 Exibições
- Última mensagem por marinalcd

Sex Mar 08, 2013 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [derivada de funçoes diferenciais]
por lucasdemirand » Qua Ago 07, 2013 00:34
- 1 Respostas
- 1492 Exibições
- Última mensagem por Russman

Qua Ago 07, 2013 15:46
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de divisão de funções trigonométricas
por Fernandobertolaccini » Ter Jul 08, 2014 17:37
- 1 Respostas
- 1358 Exibições
- Última mensagem por e8group

Ter Jul 08, 2014 17:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 . Desse modo, podemos reescrever o resultado como:
. Desse modo, podemos reescrever o resultado como: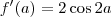
 com
com  e nem
e nem  com
com 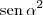 .
.


 .
.



