 por Faby » Seg Set 19, 2011 10:50
por Faby » Seg Set 19, 2011 10:50
O conjunto B delimitado pelos gráficos das retas y=x+3, y=-1, x=2 e pelos gráficos das curvas

e

.
Resolução:
Fiz o gráfico, então pensei na seguinte soma para calcular a área S
![S=\int_{-4}^{0}\left[x+3-(-1)-{x}^{2}+1 \right]dx+\int_{0}^{2}\left\left[ ({x}^{2}+1 \right)-\sqrt[]{x} \right]dx+\int_{0}^{1}\left[-\sqrt[]{x}-\left(-1 \right) \right]dx S=\int_{-4}^{0}\left[x+3-(-1)-{x}^{2}+1 \right]dx+\int_{0}^{2}\left\left[ ({x}^{2}+1 \right)-\sqrt[]{x} \right]dx+\int_{0}^{1}\left[-\sqrt[]{x}-\left(-1 \right) \right]dx](/latexrender/pictures/b890234704ea17da485ec6e8a08b0f08.png)
Estou no caminho certo?
obrigada
Editado pela última vez por
Faby em Ter Set 20, 2011 12:28, em um total de 1 vez.
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Set 19, 2011 10:58
por LuizAquino » Seg Set 19, 2011 10:58
Faby,
Por favor, poste também suas tentativas e dúvidas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Faby » Ter Set 20, 2011 13:05
por Faby » Ter Set 20, 2011 13:05
Postei minhas considerações direto na pergunta,
Como faço pra colocar o gráfico?
obrigada
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Set 21, 2011 01:11
por LuizAquino » Qua Set 21, 2011 01:11
A figura abaixo ilustra o conjunto B.
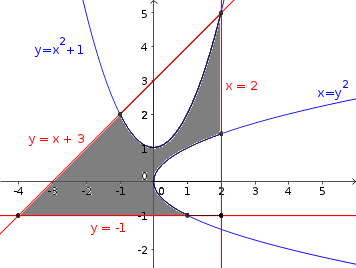
- área-B.png (10.43 KiB) Exibido 6278 vezes
Note que a área de B será dada por:

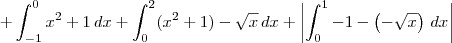
Faby escreveu:Como faço pra colocar o gráfico?
Use a opção "Adicionar um anexo" disponível durante a edição de sua mensagem.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Faby » Qua Set 21, 2011 01:54
por Faby » Qua Set 21, 2011 01:54
...vou calcular cada integral separadamente, mas agora preciso dormir,
pela manhã posto o resultado que cheguei, desde já, muito obrigada.
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Qua Set 21, 2011 20:08
por Faby » Qua Set 21, 2011 20:08
calculando as integrais separadamente, cheguei ao seguinte resultado:
![=\left|-3 \right|+2+\left|3 \right|+\frac{4}{3}+\frac{14-2\sqrt[]{8}}{3}+\left|\frac{-1}{3} \right| =\left|-3 \right|+2+\left|3 \right|+\frac{4}{3}+\frac{14-2\sqrt[]{8}}{3}+\left|\frac{-1}{3} \right|](/latexrender/pictures/a42baca35de7053ab1cfb14f8c3e2613.png)
está na ordem das integrais proposta anteriormente.
Estou no caminho?
obrigada
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Qua Set 21, 2011 23:16
por Faby » Qua Set 21, 2011 23:16
eu já tinha encontrado um erro, ficando assim
=|-3|+2+|3|+4/3+(14-4?2)/3+|-1/3|=3+2+3+4/3+(14-4?2)/3+1/3= 8+(19-4?2)/3=(24+19-4?2)/3=(43-4?2)/3
na primeira integral é que o resultado está ficando diferente, não consegui chegar a -1/2 e sim a -6/2
onde será que estou errando.
vou fazer o cálculo novamente
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Qua Set 21, 2011 23:27
por Faby » Qua Set 21, 2011 23:27
...acho que encontrei meu erro, vou calcular novamente, já mando o novo resultado pra primeira integral,
att
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Qui Set 22, 2011 00:41
por Faby » Qui Set 22, 2011 00:41
...encontrei meu erro, calculei a primitiva errada, cheguei a -1/2.
Obrigada
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de Áreas utilizando integrais
por Rambox » Ter Jun 14, 2011 14:38
- 2 Respostas
- 2208 Exibições
- Última mensagem por Rambox

Ter Jun 14, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8816 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais (áreas) [dúvida]
por citadp » Qua Jun 20, 2012 11:21
- 4 Respostas
- 3183 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- Interseção entre áreas (Integrais)
 por thejotta » Seg Abr 30, 2018 16:52
por thejotta » Seg Abr 30, 2018 16:52
- 3 Respostas
- 11209 Exibições
- Última mensagem por Gebe

Ter Mai 01, 2018 22:51
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Cálculo de áreas
por pinkfluor » Qui Jul 21, 2011 11:38
- 3 Respostas
- 2911 Exibições
- Última mensagem por pinkfluor

Qui Jul 21, 2011 17:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  .
.![S=\int_{-4}^{0}\left[x+3-(-1)-{x}^{2}+1 \right]dx+\int_{0}^{2}\left\left[ ({x}^{2}+1 \right)-\sqrt[]{x} \right]dx+\int_{0}^{1}\left[-\sqrt[]{x}-\left(-1 \right) \right]dx S=\int_{-4}^{0}\left[x+3-(-1)-{x}^{2}+1 \right]dx+\int_{0}^{2}\left\left[ ({x}^{2}+1 \right)-\sqrt[]{x} \right]dx+\int_{0}^{1}\left[-\sqrt[]{x}-\left(-1 \right) \right]dx](/latexrender/pictures/b890234704ea17da485ec6e8a08b0f08.png)

 e
e  .
.![S=\int_{-4}^{0}\left[x+3-(-1)-{x}^{2}+1 \right]dx+\int_{0}^{2}\left\left[ ({x}^{2}+1 \right)-\sqrt[]{x} \right]dx+\int_{0}^{1}\left[-\sqrt[]{x}-\left(-1 \right) \right]dx S=\int_{-4}^{0}\left[x+3-(-1)-{x}^{2}+1 \right]dx+\int_{0}^{2}\left\left[ ({x}^{2}+1 \right)-\sqrt[]{x} \right]dx+\int_{0}^{1}\left[-\sqrt[]{x}-\left(-1 \right) \right]dx](/latexrender/pictures/b890234704ea17da485ec6e8a08b0f08.png)




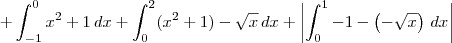


![=\left|-3 \right|+2+\left|3 \right|+\frac{4}{3}+\frac{14-2\sqrt[]{8}}{3}+\left|\frac{-1}{3} \right| =\left|-3 \right|+2+\left|3 \right|+\frac{4}{3}+\frac{14-2\sqrt[]{8}}{3}+\left|\frac{-1}{3} \right|](/latexrender/pictures/a42baca35de7053ab1cfb14f8c3e2613.png)





