 por Flashed » Ter Set 20, 2011 11:16
por Flashed » Ter Set 20, 2011 11:16
Boas
Não sei se estou no sitio certo, até porque as minhas bases a matemática não são muito boas...

Mas para o problema em questão acho que vou perceber ...
Bem a duvida é a seguinte.
Imagem um raio de 800 mm.
O centro desse raio encontra-se no ponto zero, resumindo, o inicio da circunferência é : x=0 / y= 800, e o fim da mesma é x=800 / y= 0.
Eu preciso de saber qual é o Y se o X for igual a 400?
Obviamente será menor que 800 né? Mas como chego a esse valor?
Cumps e obrigado
-
Flashed
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jul 11, 2011 08:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: gdf
- Andamento: formado
 por MarceloFantini » Ter Set 20, 2011 18:28
por MarceloFantini » Ter Set 20, 2011 18:28
Flashed, por favor coloque o enunciado inteiro, assim será mais fácil te ajudar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Flashed » Ter Set 20, 2011 18:48
por Flashed » Ter Set 20, 2011 18:48
Boas
Não tem enunciado, isto é um problema que eu desenvolvi!
Obrigado
-
Flashed
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jul 11, 2011 08:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: gdf
- Andamento: formado
 por MarceloFantini » Ter Set 20, 2011 18:55
por MarceloFantini » Ter Set 20, 2011 18:55
Bom, está mal formulado. O que seria um raio de 800mm? Circunferências tem raios, que é a distância constante que seus pontos mantém do centro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Flashed » Ter Set 20, 2011 19:30
por Flashed » Ter Set 20, 2011 19:30
O objectivo é ter um quadrado de 800 por 800 e nele é desenhada um quarto de circunferência.
Esse quadrado está nos eixos x=0 e Y=0.
A circunferência começa de x = 0 Y = 800 até X = 800 Y = 0
Entendeu a forma que estou a tentar explicar :P Fica um pouco difícil assim

Então, preciso de saber a coordenada de Y se X for igual a 400.
Cumps
-
Flashed
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jul 11, 2011 08:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: gdf
- Andamento: formado
 por MarceloFantini » Ter Set 20, 2011 19:34
por MarceloFantini » Ter Set 20, 2011 19:34
É só pensar na distância. Como é uma circunferência:

Agora coloque
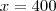
e veja o valor de y.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema de coordenadas] Coordenadas do paralelepipedo
 por rochadapesada » Dom Dez 15, 2013 15:05
por rochadapesada » Dom Dez 15, 2013 15:05
- 0 Respostas
- 1404 Exibições
- Última mensagem por rochadapesada

Dom Dez 15, 2013 15:05
Geometria Analítica
-
- coordenadas
por ulisses123 » Seg Jul 14, 2014 15:24
- 0 Respostas
- 1047 Exibições
- Última mensagem por ulisses123

Seg Jul 14, 2014 15:24
Geometria Plana
-
- coordenadas
por ulisses123 » Seg Jul 14, 2014 15:54
- 0 Respostas
- 873 Exibições
- Última mensagem por ulisses123

Seg Jul 14, 2014 15:54
Geometria Plana
-
- Coordenadas do Baricentro
por Cleyson007 » Sáb Fev 13, 2010 14:22
- 1 Respostas
- 4508 Exibições
- Última mensagem por MarceloFantini

Dom Fev 14, 2010 00:44
Geometria Analítica
-
- Coordenadas Polares
por Questioner » Sáb Jul 17, 2010 14:54
- 2 Respostas
- 4189 Exibições
- Última mensagem por Questioner

Sáb Jul 17, 2010 18:37
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






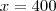 e veja o valor de y.
e veja o valor de y.