 por RenanRodrigues » Dom Set 18, 2011 15:40
por RenanRodrigues » Dom Set 18, 2011 15:40
Gente, to com uma grande duvida em um exercicio de equacao modular. se alguem puder me ajudar ficarei grato .. (desculpe se eu estiver postando em local errado, pois sou novo nesse forum)
o exercicio é esse, to com dificuldades pra começar a resolver ele, pelo fato do mesmo ter fracao no modulo ..
|10 -x/2| = 5
x/2 = x sobre 2 HEHE Fracao rs
Aguardo respostas
Obrigado
Renan
-
RenanRodrigues
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Set 18, 2011 15:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Manutencao Industrial
- Andamento: cursando
 por gvm » Seg Set 19, 2011 21:19
por gvm » Seg Set 19, 2011 21:19
É um exercício de módulo simples, independente da fração o processo de resolução é o mesmo.
Se

Então
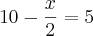
ou

Aí é só resolver
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
 por RenanRodrigues » Ter Set 20, 2011 07:02
por RenanRodrigues » Ter Set 20, 2011 07:02
Amigo, como seria a resolucao dele?
pode me ajudar
Abraçao
-
RenanRodrigues
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Set 18, 2011 15:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Manutencao Industrial
- Andamento: cursando
 por gvm » Ter Set 20, 2011 21:21
por gvm » Ter Set 20, 2011 21:21
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7390 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3410 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação modular
por amandactdas » Qui Jul 23, 2009 13:14
- 1 Respostas
- 2786 Exibições
- Última mensagem por Molina

Qui Jul 23, 2009 15:26
Funções
-
- Equação modular.
por JoaoGabriel » Sáb Set 18, 2010 11:01
- 3 Respostas
- 2499 Exibições
- Última mensagem por JoaoGabriel

Sáb Set 18, 2010 14:00
Funções
-
- Equação Modular
 por baianinha » Ter Mai 24, 2011 22:15
por baianinha » Ter Mai 24, 2011 22:15
- 2 Respostas
- 1946 Exibições
- Última mensagem por LuizAquino

Sex Mai 27, 2011 22:05
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



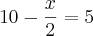

 ou
ou 
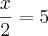

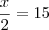

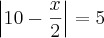 é S = {10 ; 30}
é S = {10 ; 30}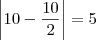
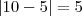
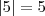 (A igualdade é verdadeira)
(A igualdade é verdadeira)

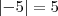 (A igualdade é verdadeira)
(A igualdade é verdadeira)