 , calcular a derivada da sua função inversa no ponto y=4.
, calcular a derivada da sua função inversa no ponto y=4.Pessoal eu estou com dificuldades para resolver este exercício, chega uma hora que parece que não tem solução.
Alguém consegue chegar na derivada da função inversa?

 , calcular a derivada da sua função inversa no ponto y=4.
, calcular a derivada da sua função inversa no ponto y=4.
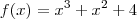 , então o exercício solicita que seja calculado
, então o exercício solicita que seja calculado ![\left[f^{-1}(4)\right]^\prime \left[f^{-1}(4)\right]^\prime](/latexrender/pictures/4df208034767e862f83fbb9caad76168.png) .
.

carvalhothg escreveu:A duvida é, como isolar g(y) para poder derivar ele. Tem alguma dica?


carvalhothg escreveu:muito obrigado, pois nem no livro que estou utilizando (Calculo A - Diva Flemming) tinha encontrado aquele método de se calcular a derivada inversa de uma função...
carvalhothg escreveu:E parabéns por este seu trabalho brilhante.



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes