 por marciommuniz » Qua Abr 08, 2009 21:04
por marciommuniz » Qua Abr 08, 2009 21:04
Olá equipe ajudamatematica.com
Espero que tenham um pouco de paciencia comigo, meu prof. de calculo I é cubano e nao entendo nada que ele fala ahahhaha

Gostaria de saber a resolucao do seguinte limite

Não sei nem por onde começar com esse logaritmo neperiano
HEEELP!

"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por marciommuniz » Qua Abr 08, 2009 22:00
por marciommuniz » Qua Abr 08, 2009 22:00
Bem pelo oq eu sei
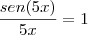
Eu poderia usar L'Hospital (pag 245 - GUIDORIZZI) para resolver o logaritmo neperiano??
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-

marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por Molina » Qui Abr 09, 2009 13:47
por Molina » Qui Abr 09, 2009 13:47
Boa tarde, Márcio.
Para você resolver o logaritmo neperiano (
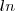
) você precisa ter noção de Regra da Cadeia. Dá uma lida neste site:
http://ecalculo.if.usp.br/derivadas/pop ... cadeia.htm e caso você nao consiga mesmo assim resolver, coloque até que ponto você chegou.
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Marcampucio » Qui Abr 09, 2009 14:06
por Marcampucio » Qui Abr 09, 2009 14:06
Usando a propriedade de que
![\lim[f(x)+g(x)]=\lim f(x)+\lim g(x) \lim[f(x)+g(x)]=\lim f(x)+\lim g(x)](/latexrender/pictures/97d7a429c3760559fe6e0be23daac255.png)
, teremos no segundo termo

. Precisamos nos concentrar no primeiro limite:

em que podemos aplicar l'Hopital
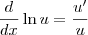

, então

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por marciommuniz » Qui Abr 09, 2009 14:29
por marciommuniz » Qui Abr 09, 2009 14:29
Obrigado pela ajuda. Realmente eu encontrei a mesma resposta usando L'Hopital mas não
sabia que era possível usá-lo.
Gostei muito desse fórum, vou participar mais vezes
Um abraço.
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-

marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por Molina » Qui Abr 09, 2009 15:45
por Molina » Qui Abr 09, 2009 15:45
Que bom que você entendeu, Márcio.
Quando tiver outras dúvidas basta criar outros tópicos que sempre que for possível alguem vai te ajudar!
No mais, bom feriado e bom estudo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- limite.como calculo esse limite?
por jeffinps » Ter Mar 12, 2013 12:07
- 1 Respostas
- 2258 Exibições
- Última mensagem por Douglas16

Ter Mar 12, 2013 14:27
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] AJUDA Calculo de Limite
por will94 » Ter Mai 22, 2012 20:32
- 1 Respostas
- 2231 Exibições
- Última mensagem por LuizAquino

Qua Mai 23, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3335 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] calculo de limite trigonométrico
por PRADO » Dom Mai 22, 2016 17:01
- 2 Respostas
- 5631 Exibições
- Última mensagem por PRADO

Sex Jun 03, 2016 23:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






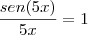

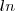 ) você precisa ter noção de Regra da Cadeia. Dá uma lida neste site: http://ecalculo.if.usp.br/derivadas/pop ... cadeia.htm e caso você nao consiga mesmo assim resolver, coloque até que ponto você chegou.
) você precisa ter noção de Regra da Cadeia. Dá uma lida neste site: http://ecalculo.if.usp.br/derivadas/pop ... cadeia.htm e caso você nao consiga mesmo assim resolver, coloque até que ponto você chegou.

![\lim[f(x)+g(x)]=\lim f(x)+\lim g(x) \lim[f(x)+g(x)]=\lim f(x)+\lim g(x)](/latexrender/pictures/97d7a429c3760559fe6e0be23daac255.png) , teremos no segundo termo
, teremos no segundo termo  . Precisamos nos concentrar no primeiro limite:
. Precisamos nos concentrar no primeiro limite: em que podemos aplicar l'Hopital
em que podemos aplicar l'Hopital 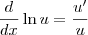
 , então
, então




