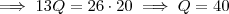[Sistema de equações] duvidas

por **DELTAPI** » Sex Set 16, 2011 14:56

Alguem poderia me auxiliar a montar este sistema de equações:

Joana foi à feira levando certa quantia em dinheiro. Na 1.ª banca, comprou legumes e gastou 1/4 dessa quantia. Na 2.ª banca, comprou verduras e gastou 2/5 do valor gasto na 1.ª banca. Na 3.ª banca, comprou frutas e gastou R$ 15,50. Sabendo-se que da quantia inicial restaram R$ 10,50, conclui-se que na compra de verduras ela gastou?

x= valor de dinheiro qeu levou

1ª Banca = x-(1/4x)
2ª Banca = 2/5 (x -1/4x)
3ª banca = R$15,50
sobrou RS10,50
Montei a equação da seguinte forma mas não deu o resultado proposto: alguem pode indicar onde eu errei?
x-(1/4x)-2/5(x-1/4)-15,50=10,50

por **Neperiano** » Sex Set 16, 2011 15:25

Ola

Transforme esse 1/4 em 0,25

Logo na 1 banca gastou 0,25
Na 2 banca gastou 2/5 de 0,25 que é 0,1 (só fazer 0,25 vezes 2 e dividido por 5)
Na 3 banca gastou 15,50

Sobrou 10,50 de tudo entao

Ela tinha 15,50+10,50=26 reais mais 0,35

Então

26 - 1
x - 0,35

Logo 9,1
Então ela tinha 26+9,1= 35,1 reais

Acho que é isso

Atenciosamente

por **MarceloFantini** » Sex Set 16, 2011 17:20

Seja Q a quantia inicial. Primeiro, gastou $\frac{Q}{4}$ ; depois, gastou dois quintos do que gastou primeiro, logo $\frac{2}{5} \cdot \frac{Q}{4} = \frac{Q}{10}$ ; por último, gastou 15,50 e sobrou 10,50. Equacionando:

$Q - \frac{Q}{4} - \frac{Q}{10} - 15,50 = 10,50 \implies 20Q - 5Q - 2Q = 26 \cdot 20 \implies$

$\implies 13Q = 26 \cdot 20 \implies Q = 40$

por **DELTAPI** » Sáb Set 17, 2011 10:12

PESSOAL, MUITO OBRIGADO.
NA SEGUNDA BANCA ELE GASTOU R$4,00 ( Q/10 =>R$4,00).
CASO CONHEÇAM ALGUM LIVRO QUE ENSINA COMO MONTAR AS EQUAÇÕES, FAVOR ME INDICAR.