 por carvalhothg » Ter Set 13, 2011 15:43
por carvalhothg » Ter Set 13, 2011 15:43
Como resolver o exercício abaixo sem uso de computador, ou seja, como encontrar o valor de x na munheca?
Pois estou tentando usar ln mas chega uma hora que eu travo, poderiam me ajudar?
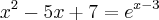
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Neperiano » Ter Set 13, 2011 18:23
por Neperiano » Ter Set 13, 2011 18:23
Ola
Coloque o ln nos dois lados da equação vai ficar
Ln(função)=x-3
Mostre o que você fez para que possamos dar uma olhada
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Ter Set 13, 2011 19:27
por MarceloFantini » Ter Set 13, 2011 19:27
Poste o enunciado. Isto me parece aquelas questões que perguntam quantas raízes existem para a equação e claramente não pede a questão analiticamente pois é muito difícil/aproximada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Set 13, 2011 22:21
por LuizAquino » Ter Set 13, 2011 22:21
carvalhothg escreveu:Como resolver o exercício abaixo sem uso de computador, ou seja, como encontrar o valor de x na munheca?
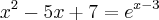
Essa é uma
equação transcendental. Tipicamente, as equações transcendentais não possuem solução analítica. Isto é, usando a sua expressão: não dá para resolver "
na munheca" essas equações. Portanto, é necessário aplicar métodos numéricos ou gráficos para resolvê-las. Entretanto, uma primeira estratégia é procurar por soluções triviais.
Note que o valor mais trivial que podemos pensar para o segundo membro da equação é quando x = 3, pois teremos
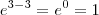
. Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que
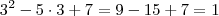
. Logo, x = 3 é uma solução dessa equação.
Se houver outra solução, então ela não é mais trivial e algum método numérico ou gráfico deve ser aplicado. Por exemplo, aplicando o
Método de Newton podemos encontrar que outra raiz dessa equação é aproximadamente x = 4,7933.
Aproveito ainda para lembrar que nos cursos de graduação da área de exatas há uma disciplina chamada Cálculo Numérico. Um dos objetivos dessa disciplina é exatamente aprender técnicas numéricas que permitem calcular a solução de equações como essa.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carvalhothg » Ter Set 13, 2011 22:48
por carvalhothg » Ter Set 13, 2011 22:48
LuizAquino escreveu:carvalhothg escreveu:Como resolver o exercício abaixo sem uso de computador, ou seja, como encontrar o valor de x na munheca?
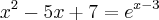
Essa é uma
equação transcendental. Tipicamente, as equações transcendentais não possuem solução analítica. Isto é, usando a sua expressão: não dá para resolver "
na munheca" essas equações. Portanto, é necessário aplicar métodos numéricos ou gráficos para resolvê-las. Entretanto, uma primeira estratégia é procurar por soluções triviais.
Note que o valor mais trivial que podemos pensar para o segundo membro da equação é quando x = 3, pois teremos
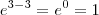
. Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que
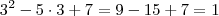
. Logo, x = 3 é uma solução dessa equação.
Se houver outra solução, então ela não é mais trivial e algum método numérico ou gráfico deve ser aplicado. Por exemplo, aplicando o
Método de Newton podemos encontrar que outra raiz dessa equação é aproximadamente x = 4,7933.
Aproveito ainda para lembrar que nos cursos de graduação da área de exatas há uma disciplina chamada Cálculo Numérico. Um dos objetivos dessa disciplina é exatamente aprender técnicas numéricas que permitem calcular a solução de equações como essa.
Aquino,
primeiramente muito obrigado pela ajuda....sem quer abusar muito da sua boa vontade...você poderia ensinar a utilizar este método de newton?
-
carvalhothg
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Dom Set 04, 2011 18:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Qua Set 14, 2011 00:06
por LuizAquino » Qua Set 14, 2011 00:06
carvalhothg escreveu:Aquino,
primeiramente muito obrigado pela ajuda....sem quer abusar muito da sua boa vontade...você poderia ensinar a utilizar este método de newton?
É mais interessante que você procure por um livro de Cálculo Numérico. Ou ainda, visite o endereço indicado pelo colega Fantini. Há também um vasto material disponível na internet ensinando a usar esse método. Eu recomendo que você faça uma pesquisa. Com certeza você vai encontrar muito material.

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como encontrar o valor de b?
por Cleyson007 » Sáb Mai 25, 2013 16:55
- 1 Respostas
- 1773 Exibições
- Última mensagem por e8group

Sáb Mai 25, 2013 18:59
Números Complexos
-
- Como encontrar o valor de uma matriz binaria
por oescolhido » Seg Fev 18, 2013 20:19
- 1 Respostas
- 2982 Exibições
- Última mensagem por marcos chaves

Qua Abr 03, 2013 21:43
Matrizes e Determinantes
-
- [Encontrar valor A, B e C]
por engrobson » Dom Out 06, 2013 17:14
- 0 Respostas
- 1286 Exibições
- Última mensagem por engrobson

Dom Out 06, 2013 17:14
Equações
-
- [Matriz] Encontrar o Valor de X
por Myneyrynho » Qui Set 04, 2014 12:24
- 1 Respostas
- 12757 Exibições
- Última mensagem por jcmatematica

Sáb Set 27, 2014 16:09
Matrizes e Determinantes
-
- [ Equação de 3º Grau ] Encontrar valor de máximo relativo
por Fabio Ribeiro » Qui Jun 05, 2014 12:30
- 4 Respostas
- 8861 Exibições
- Última mensagem por Fabio Ribeiro

Sáb Jun 07, 2014 18:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
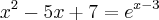

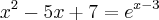




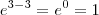 . Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que
. Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que 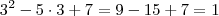 . Logo, x = 3 é uma solução dessa equação.
. Logo, x = 3 é uma solução dessa equação.
. Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que
. Logo, x = 3 é uma solução dessa equação.










