Encontrei este problema numa prova de vestibular:
(UnB-DF)Na física newtoniana, as regras para relacionar a posição
x e o tempo t, medidos a partir de um sistema de coordenadas em
repouso — S —, com a posição x’ e o tempo t’, medidos a partir
de um sistema — S’ — que se move com velocidade V, com
relação ao sistema S, são dadas pelas equações x’ = x – Vt e t’ = t,
que são denominadas transformações de Galileu. Com o advento
da teoria da relatividade especial proposta por Einstein, essas
regras, com o nome de transformações de Lorentz, passaram a ser
dadas por: x’ =
 ; t’ =
; t’ =  , em que
, em que ![\gamma = \frac{1}{\sqrt[]{1 - \frac{V^2}{c^2}}} \gamma = \frac{1}{\sqrt[]{1 - \frac{V^2}{c^2}}}](/latexrender/pictures/f9314637b3f18d228b33d605814bbac1.png) e c = 300.000 km/s corresponde à velocidade da luz no vácuo,
e c = 300.000 km/s corresponde à velocidade da luz no vácuo,medida segundo qualquer referencial inercial, pois c é um valor
absoluto. A distância que a luz percorre no vácuo em um ano,
considerando-se que o ano tenha 365 dias e 6 h, é definida como
ano-luz e utilizada para expressar distâncias entre corpos celestes.
Julgue o item abaixo:
Se v’ = x’/t’ e v = x/t, então a relação entre essas velocidades, de acordo com as transformações de Lorentz, é v’ =
 , não sendo possível, segundo tais transformações, encontrar velocidade v’ maior que a velocidade da luz.
, não sendo possível, segundo tais transformações, encontrar velocidade v’ maior que a velocidade da luz.Tentei resolver o problema de a seguinte maneira:
v’ =
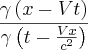 . Anulando-se os coeficientes
. Anulando-se os coeficientes  , fiquei com
, fiquei com  . Em seguida,
. Em seguida, 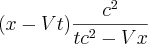 . A partir daí, não sei como simplificar mais a equação para poder julgar o item. Estou preso neste exercício há alguns dias, e qualquer ajuda será apreciada.
. A partir daí, não sei como simplificar mais a equação para poder julgar o item. Estou preso neste exercício há alguns dias, e qualquer ajuda será apreciada.Obrigado.

