 por Aliocha Karamazov » Seg Set 12, 2011 01:27
por Aliocha Karamazov » Seg Set 12, 2011 01:27
Caros, vou postar o exercício e minha resolução. O post ficou um pouco maior do que é de costume, porque eu fiz questão de colocar todas as passagens, uma vez que, pelo fato de minha resposta estar "quase" certa, provavelmente eu errei em alguma passagem. Parece complicado, mas não é. Gostaria da colaboração de alguém para que eu possa saber onde e por que errei.
Dado
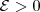
arbitrário, determine
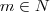
* tal que

para todo
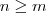
, onde
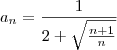
e
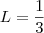
Eu fiz dessa maneira:
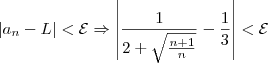
Mas,
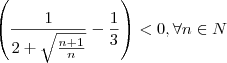
* (Isso é fácil provar, mas eu omiti para encurtar). Portanto,
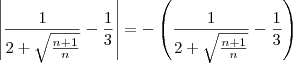
Voltando à inequação:
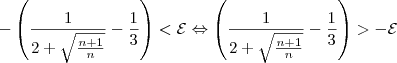
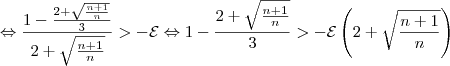
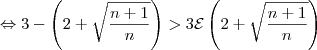
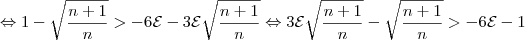
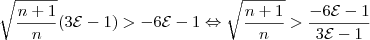
Agora, é preciso elevar ambos lados ao quadrado. No entanto, o membro à direita é negativo para alguns valores de
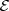
. Resolvendo a inequação
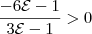
, encontra-se
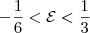
.
Elevando-se ambos os lados ao quadrado, segue que:
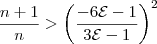
Com mais algumas manipulações algébricas, (omitidas para não deixar o post ainda mais extenso), chega-se em:
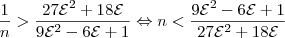
No gabarito, está
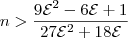
Realmente, não faz sentido chegar a um resultado em que n deve ser menor do que alguma coisa, pois o enunciado pede um

tal que
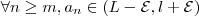
Gostaria que alguém apontasse onde eu errei.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Aliocha Karamazov » Seg Set 12, 2011 14:32
por Aliocha Karamazov » Seg Set 12, 2011 14:32
Obrigado, MarceloFantini. Ficou bem claro, consegui reproduzir sua resolução. Acho que não vale mais a pena tentar encontrar onde eu errei, teve ter sido em alguma passagem...
Agora deu certo!
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6344 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7401 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3743 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2121 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1629 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
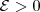 arbitrário, determine
arbitrário, determine 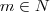 * tal que
* tal que  para todo
para todo 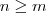 , onde
, onde 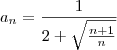 e
e 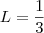
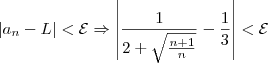
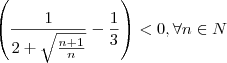 * (Isso é fácil provar, mas eu omiti para encurtar). Portanto,
* (Isso é fácil provar, mas eu omiti para encurtar). Portanto, 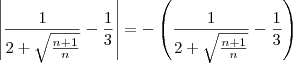
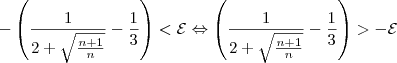
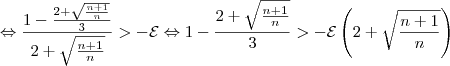
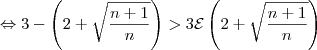
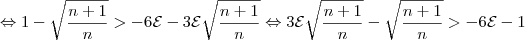
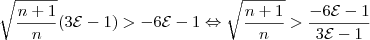
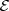 . Resolvendo a inequação
. Resolvendo a inequação 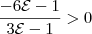 , encontra-se
, encontra-se 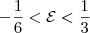 .
.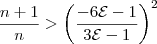
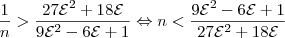
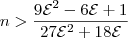
 tal que
tal que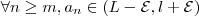


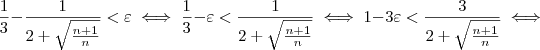
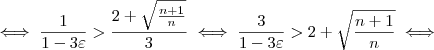
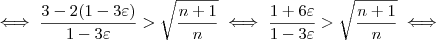
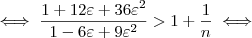
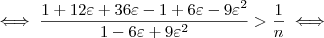
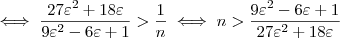




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.