



 , onde P(x) e Q(x) são polinômios. Nesse caso, em particular, é comum e muito prático analisar o domínio da função, e se existe algum ponto x onde a função não está definida no domínio, então esse ponto supostamente será uma assíntota vertical. É sempre indispensável e necessário fazer a verificação dessa observação pelos limites laterais no(s) ponto(s) em que f não está definida, e se f(x) tende a menos ou mais infinito, conclui-se que, de fato, aquele ponto é uma assíntota vertical.
, onde P(x) e Q(x) são polinômios. Nesse caso, em particular, é comum e muito prático analisar o domínio da função, e se existe algum ponto x onde a função não está definida no domínio, então esse ponto supostamente será uma assíntota vertical. É sempre indispensável e necessário fazer a verificação dessa observação pelos limites laterais no(s) ponto(s) em que f não está definida, e se f(x) tende a menos ou mais infinito, conclui-se que, de fato, aquele ponto é uma assíntota vertical.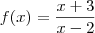 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

