 por beel » Sáb Set 03, 2011 22:11
por beel » Sáb Set 03, 2011 22:11
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Dom Set 04, 2011 13:52
por beel » Dom Set 04, 2011 13:52
O limite e é elevado a constante? ( e^b)?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Set 04, 2011 17:12
por LuizAquino » Dom Set 04, 2011 17:12
Você tem o limite:
Fazendo a substituição u = Mx (e portanto

), veja que quando x tende para 0, u também tende para zero. Desse modo, podemos reescrever o limite como:

Mas, sabemos que isso é o mesmo que:
![\lim_{u \to 0} \left[{(1+ u)}^{\frac{1}{u}}\right]^M \lim_{u \to 0} \left[{(1+ u)}^{\frac{1}{u}}\right]^M](/latexrender/pictures/77d7f0de39076e03e8815ef44ad86384.png)
Das propriedades dos limites sabemos que isso é igual a:
![\left[\lim_{u \to 0} {(1+ u)}^{\frac{1}{u}}\right]^M \left[\lim_{u \to 0} {(1+ u)}^{\frac{1}{u}}\right]^M](/latexrender/pictures/d426df3fdbc95bcb709a004359d74958.png)
Veja que esse limite tem como resultado

.
Portanto, temos que
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Set 04, 2011 17:25
por beel » Dom Set 04, 2011 17:25
Obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Limite fundamental Exponencial
por antonelli2006 » Ter Set 20, 2011 05:54
- 1 Respostas
- 2027 Exibições
- Última mensagem por LuizAquino

Ter Set 20, 2011 12:22
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental
por matmatco » Qui Set 01, 2011 11:04
- 6 Respostas
- 3458 Exibições
- Última mensagem por matmatco

Qui Set 08, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- [limite fundamental]
por TheKyabu » Qui Out 25, 2012 18:33
- 1 Respostas
- 1718 Exibições
- Última mensagem por TheKyabu

Qui Out 25, 2012 18:50
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental
por Julia Maia » Seg Abr 25, 2016 14:17
- 0 Respostas
- 2083 Exibições
- Última mensagem por Julia Maia

Seg Abr 25, 2016 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Limite Fundamental
por Everton Pire Souza » Dom Abr 30, 2017 23:58
- 0 Respostas
- 2959 Exibições
- Última mensagem por Everton Pire Souza

Dom Abr 30, 2017 23:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ), veja que quando x tende para 0, u também tende para zero. Desse modo, podemos reescrever o limite como:
), veja que quando x tende para 0, u também tende para zero. Desse modo, podemos reescrever o limite como:
![\lim_{u \to 0} \left[{(1+ u)}^{\frac{1}{u}}\right]^M \lim_{u \to 0} \left[{(1+ u)}^{\frac{1}{u}}\right]^M](/latexrender/pictures/77d7f0de39076e03e8815ef44ad86384.png)
![\left[\lim_{u \to 0} {(1+ u)}^{\frac{1}{u}}\right]^M \left[\lim_{u \to 0} {(1+ u)}^{\frac{1}{u}}\right]^M](/latexrender/pictures/d426df3fdbc95bcb709a004359d74958.png)
 .
.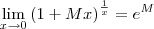



 .
.



