 por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
pessoal estou com duvida nesta questao.. nao estou conseguindo monta o problema..
Das 182 páginas de um relatório, digitadas por Adilson, Benilson e Cevilson, sabe-se que: o número das digitadas por Adilson correspondia a 2/3 do número das digitadas por Benilson; o número das digitadas por Benilson, a 11/12 das digitadas por Cevilson. Quantas páginas Cevilson digitou a mais do que Benilson?
resp. 6
Abraço.. André
-
ANDRE RENATO PROFETA
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Fev 14, 2009 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Contabeis
- Andamento: formado
 por Molina » Sex Mar 13, 2009 14:58
por Molina » Sex Mar 13, 2009 14:58
Boa tarde, André.
Vamos usar as variáveis A para Adilson, B para Benilson e C para Cevilson.
Assim, como diz o enunciado do problema:
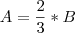


Da primeira com a segunda expressão temos que:
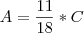
Jogando tudo na terceira expressão, para ficar tudo em função de C, temos:
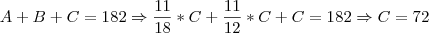
Utilizando a segunda expressão novamente, temos:
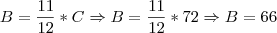
Logo

Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10721 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9732 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4612 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6537 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
-
- Problema
por DanielFerreira » Ter Set 22, 2009 14:15
- 2 Respostas
- 2116 Exibições
- Última mensagem por DanielFerreira

Qui Set 24, 2009 21:31
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


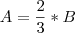


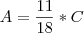
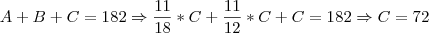
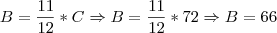




 .
.
 :
: