eu to com uma dificuldade muito grande em calcular área por integral,
a questão é a seguinte:
Determine a área limitada pela parábora y =
 e pela reta y =
e pela reta y = 
Gráfico :

A resposta é 4,5. Mas não conseguir encontrar de jeito nenhum a resposta certa.
o link da imagem do gráfico caso haja problema na de cima.
http://imageshack.us/photo/my-images/819/grfico2i.jpg/
Agradeço a todos desde já



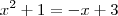
 para
para ![x\in [-2,\, 1] x\in [-2,\, 1]](/latexrender/pictures/827a169ef687cf6140e6899db2883074.png) .
.


 .
.
 :
: