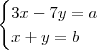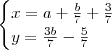por 380625 » Sáb Ago 20, 2011 16:08
por 380625 » Sáb Ago 20, 2011 16:08
Boa tarde queria uma dica para resolver os seguinte exercicio.
1) Determinar os valores de a e b que tornam o sistema
3x - 7y = a
x + y = b
5x + 3y = 5a + 2b
x + 2y = a + b - 1
compativel e determinado. Em seguida resolver o sistema.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Dom Ago 28, 2011 00:32
por LuizAquino » Dom Ago 28, 2011 00:32
380625 escreveu:1) Determinar os valores de a e b que tornam o sistema
3x - 7y = a
x + y = b
5x + 3y = 5a + 2b
x + 2y = a + b - 1
compativel e determinado. Em seguida resolver o sistema.
Um sistema é compatível e determinado quando possui apenas uma solução.
Temos o sistema:

Vamos separar esse sistema em dois:
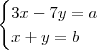

Resolvendo esses sistemas em x e y, obtemos:

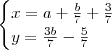
Desejamos que esses dois sistemas possuam a mesma (e única) solução. Desse modo, temos que a e b devem ser tais que:

Resolvendo esse sistema, você determina a e b. Em seguida, basta substituir esses valores nas soluções de um dos dois sistema e você determina x e y.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3081 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Funções] dificuldade para resolver
por tiaguito » Seg Out 22, 2012 17:01
- 1 Respostas
- 1831 Exibições
- Última mensagem por Russman

Seg Out 22, 2012 18:35
Funções
-
- Função Resolver esse sistema
por osmarioe » Sex Ago 14, 2015 18:29
- 2 Respostas
- 2791 Exibições
- Última mensagem por osmarioe

Sex Ago 14, 2015 21:23
Funções
-
- Como resolver esse sistema linear
por Silva339 » Qua Mar 20, 2013 18:14
- 1 Respostas
- 1863 Exibições
- Última mensagem por Russman

Qua Mar 20, 2013 18:46
Sistemas de Equações
-
- Preciso saber a fórmula para resolver esse exercício
por Dankaerte » Qui Ago 27, 2009 14:19
- 1 Respostas
- 6966 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 14:58
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.