Bom dia,
Estou usando o livro Cálculo - Funções de uma e várias variáveis. Morettin, Bussab e Hazzan
O exercício no qual estou com dúvida é o número 30 do capítulo 6 - Aplicações de Derivadas. O enunciado é o seguinte:
Um banco capta dinheiro pagando a seus aplicadores uma taxa anual de juros igual a i e repassa esse valor à taxa de 24% ao ano. Sabendo-se que a quantia captada C é dada por C = 1000i, obtenha o valor de i que maximiza o lucro anual do banco.
Eu tentei usar a fórmula de juros compostos FV = PV(1+i)^n, mas não consegui interpretar o problema a ponto de passar disso.
Alguém pode me ajudar?
Obrigado.



 ;
;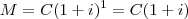 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)