Meu problema é o seguinte, antes eu cursava ensino médio profissionalizante e no meio do ano mudei pro academico, por isso eu não aprendi módulo, ou seja, não tenho nenhuma base sobre módulo e queria que alguem me ajudasse explicando passo a passo.
Resolva em R as seguintes equações:
a)
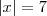acho que S={7, -7}, o que é meio obvio, mas coloquei só para confirmar. =)b)
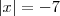
c)
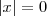
d)
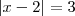
e)
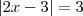
f)
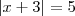
g)
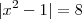
h)
i)
Resolvendo a equação
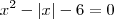você encontrará 2 raízes. Sabendo que essas 2 raízes também são raízes de 
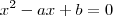calcule os valores de 
e 
.O que obtive da 1ª equação foi 2 e 3, mas não sei se esta certo por causa do módulo. Mas no final descobri que a = 5 e b = 6, mas esta errado, pois a resposta é a = 0 e b = -9
e tem só mais uma que não consegui (já to abusando rsrsrs):
Resolva em R:
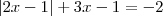
Se vocês acham que só fazendo as primeiras eu consigo fazer o resto me expliquem só as primeiras mesmo, pra mim poder praticar resolvendo as restantes.
Muito obrigado mesmo a quem puder ajudar.
, avisa que eu resolvo.
