 por Thauan_Barcellos » Sáb Ago 20, 2011 11:57
por Thauan_Barcellos » Sáb Ago 20, 2011 11:57
tenho uma função :
- Código: Selecionar todos
f( x ) = x² - 6x + 8
até ai tudo bem , continuo desenvolvendo a função :
- Código: Selecionar todos
a = 1 , b=-6 , c= 8
a= 1 > 0 ( C )
x² - 6x + 8 , F( x ) = 0
x² - 6x + 8 =0
Agora que entra a dúvida , to usando este método que o meu professor me ensinou ( Ja sei fazer por delta também ) , fico na dúvida de qual que esta certo

.
- Código: Selecionar todos
S( 2 + 4 ) = 6 ou S((-2) + (-4) ) = -6
P( 2 x 4 ) =8 P( (-2) x (-4) ) = 8
-
Thauan_Barcellos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 20, 2011 11:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Ago 20, 2011 13:44
por Molina » Sáb Ago 20, 2011 13:44
Boa tarde, Thauan.
Este método que seu professor te ensinou chama-se
Soma e Produto. Ele diz que a soma das raízes é igual a
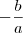
e o produto destas mesmas raízes é

. Resumindo, temos que:

Do seu problema temos que:

Ou seja, a única resposta que temos é:


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Thauan_Barcellos » Sáb Ago 20, 2011 13:51
por Thauan_Barcellos » Sáb Ago 20, 2011 13:51
Muito Obrigado , acredito que este simples detalhe tenha causado a minha duvida , duvida Respondida.
-
Thauan_Barcellos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 20, 2011 11:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9243 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2634 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2018 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2097 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8042 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.

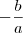 e o produto destas mesmas raízes é
e o produto destas mesmas raízes é  . Resumindo, temos que:
. Resumindo, temos que:





 , avisa que eu resolvo.
, avisa que eu resolvo.

