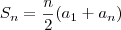Progressão Aritmética

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Progressão Aritmética

Regras do fórum
Responder

Progressão Aritmética

Mensagempor edersonubm » Sex Ago 19, 2011 11:48

João começou a juntar dinheiro para comprar um computador novo, cujo preço é de R$ 4.000,00. No 1° mês ele guardou R$ 20,00, no 2º R$ 30,00 e no 3º R$ 40,00 e assim sucessivamente sempre aumentando R$ 10,00 em relação ao mês anterior. Em quantos meses ele conseguiu juntar dinheiro para comprar o computador?
A) 30
B) 27 - gabarito
C) 25
D) 28
E) 26

Grato.
edersonubm
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Qui Jan 20, 2011 11:15
Formação Escolar: GRADUAÇÃO
Área/Curso: Administração
Andamento: formado
Voltar ao topo

Re: Progressão Aritmética

Mensagempor Molina » Sex Ago 19, 2011 12:34

Bom dia.

Há duas fórmulas para usar em problemas envolvendo Progressão Geométrica:

a_n=a_1+(n-1) \cdot r (termo geral)

e

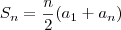S_n=\frac{n}{2}(a_1+a_n) (soma dos termos)

Tente fazer uma união dessas duas fórmulas.

Coloque suas tentativas para que possamos ver onde você está errando.


Bom estudo :y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo
Responder

Voltar para Progressões

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum