para trás e novamente viu a torre, agora sob um angulo de 25 Graus.
Supondo esses dados qual a latura da torre ?
Bom! fiz dessa forma e tambem análogo a outros que mandei
mas não tem jeito, da errada!
A forma que fiz foi a seguinte
tg
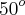 =
= 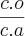
 1,19 =
1,19 = 
tg
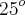 =
= 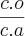
 0,46 =
0,46 = 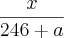
Temos:
 1,19 =
1,19 = 
 0,46 =
0,46 = 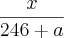
Da primeira equação temos:
 =
=  1,19
1,19Entroduzindo o resultado da primeira equação na segundo temos:
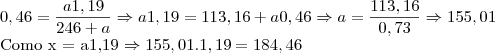
Mas a resposta correta tem que ser 188 unidades
Gostaria que olhasse na onde errei ou se fiz a questão
totalmete errada! Obrigado!



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.