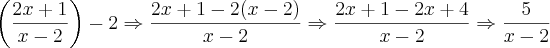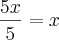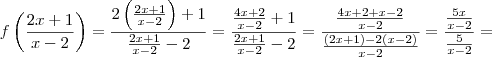por kael » Qui Mar 05, 2009 16:30
por kael » Qui Mar 05, 2009 16:30
Boa tarde.
Estou com uma duvida em uma das questões de meu trabalho escolar, gostaria de uma explicação, pois não consegui entender a do professor.
Eis a questão:
Se

, então
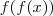
vale:
* minha resolução foi:
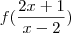
=
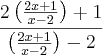
=

=

Gostaria que alguem pudesse verificar r se está correto, e me explicar mais detalhadamente esse exercício. Agradeço desde já!

-
kael
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mar 05, 2009 14:56
- Localização: Goiânia
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Mar 05, 2009 21:25
por Molina » Qui Mar 05, 2009 21:25
Boa noite, Kael.
Acho que do passo
(#) para o passo
(##) você se equivocou no
denominador da fração:
kael escreveu:(#) 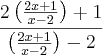
=
(##) 
=
Note que:
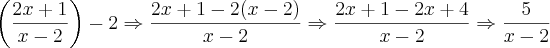
Fazendo esta correção você chegará que a resposta é
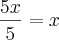
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por kael » Qui Mar 05, 2009 21:45
por kael » Qui Mar 05, 2009 21:45
Muito obrigado Molina
-
kael
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mar 05, 2009 14:56
- Localização: Goiânia
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Mar 06, 2009 12:47
por Molina » Sex Mar 06, 2009 12:47
Está certo kael. Só falto no final simplificar o

Abraços e volte sempre.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- questão função
por sheila » Qui Set 06, 2007 22:37
- 4 Respostas
- 7818 Exibições
- Última mensagem por admin

Ter Set 11, 2007 16:39
Funções
-
- Questao de Funçao
por leilahomsi » Qua Jan 09, 2013 19:19
- 1 Respostas
- 1308 Exibições
- Última mensagem por e8group

Qua Jan 09, 2013 22:38
Funções
-
- [Questão de Função]
por zanotto » Sex Mar 21, 2014 23:18
- 3 Respostas
- 2211 Exibições
- Última mensagem por Russman

Sáb Mar 22, 2014 01:22
Funções
-
- QUESTÃO DE FUNÇÃO DA UFJF
por Maira » Sáb Dez 19, 2009 16:47
- 3 Respostas
- 3030 Exibições
- Última mensagem por Maira

Sáb Dez 19, 2009 19:27
Funções
-
- Questão de Função (UFRJ)
por Carolziiinhaaah » Qui Ago 12, 2010 11:34
- 1 Respostas
- 2729 Exibições
- Última mensagem por Douglasm

Qui Ago 12, 2010 13:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , então
, então 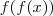 vale:
vale: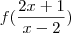 =
= 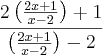 =
=  =
=