por LuizCarlos » Qui Ago 11, 2011 12:41
-
LuizCarlos
- Colaborador Voluntário
-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
por Molina » Qui Ago 11, 2011 13:52
Boa tarde, Luiz.
Você se confundiu na fração elevado a quarta potência, veja:
LuizCarlos escreveu: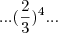
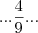
Na verdade,
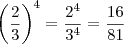
Entendido?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
por LuizCarlos » Qui Ago 11, 2011 14:43
Molina escreveu:Boa tarde, Luiz.
Você se confundiu na fração elevado a quarta potência, veja:
LuizCarlos escreveu: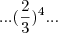
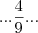
Na verdade,
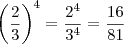
Entendido?
Valeu Diego, meu problema em matematica é isso, eu sei até fazer, mas sempre eu deixo algo por falta de atenção.
-
LuizCarlos
- Colaborador Voluntário
-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Está, ou não está certo. Eis a questão!
por Thiago 86 » Dom Set 29, 2013 21:48
- 0 Respostas
- 2848 Exibições
- Última mensagem por Thiago 86
Dom Set 29, 2013 21:48
Funções
-
- CONFERIR SE ESTÁ CERTO
por gabimucedola » Sex Abr 02, 2010 18:11
- 1 Respostas
- 1579 Exibições
- Última mensagem por davi_11
Sáb Abr 03, 2010 13:37
Matemática Financeira
-
- Isso está certo ???
por Guill » Dom Abr 08, 2012 18:21
- 5 Respostas
- 2823 Exibições
- Última mensagem por nietzsche
Dom Abr 08, 2012 19:20
Cálculo: Limites, Derivadas e Integrais
-
- Limites - Está certo?
por iceman » Dom Set 16, 2012 14:57
- 1 Respostas
- 1501 Exibições
- Última mensagem por young_jedi
Dom Set 16, 2012 16:17
Cálculo: Limites, Derivadas e Integrais
-
- simplifiquei e achei...está certo?????????????
por zig » Sex Set 23, 2011 13:57
- 3 Respostas
- 83924 Exibições
- Última mensagem por fraol
Dom Dez 11, 2011 20:24
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![(\frac{2}{3})^-2 . (\frac{2}{3})^4 + [(\frac{1}{3})^2]^3 : 3^-4](/latexrender/pictures/28458060d198d5741628ef33a01048b9.png "(\frac{2}{3})^-2 . (\frac{2}{3})^4 + [(\frac{1}{3})^2]^3 : 3^-4")
![(\frac{3}{2})^2 . (\frac{2}{3})^4 + [(\frac{1}{3})^2]^3 : 3^-4](/latexrender/pictures/9e7257cbf3d5e2da361e3b956bee3b45.png "(\frac{3}{2})^2 . (\frac{2}{3})^4 + [(\frac{1}{3})^2]^3 : 3^-4")
![\frac{1}{1} + [(\frac{1}{3})^6 : (\frac{1}{3})^4]](/latexrender/pictures/8eeea3e0231a2880cb276ef401c93cb9.png "\frac{1}{1} + [(\frac{1}{3})^6 : (\frac{1}{3})^4]")
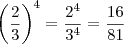
![\frac{1}{1} + [(\frac{1}{3})^(6- 4) = (\frac{1}{3})^2]](/latexrender/pictures/713c1ccbc87a2d88bbc67db253700209.png "\frac{1}{1} + [(\frac{1}{3})^(6- 4) = (\frac{1}{3})^2]")
