Sejam f e g duas funções tais que f(x) = ?x e f(g(x-1)) = 2x+1. Assinale a alternativa que representa uma afirmação correta referente à função g mencionada.
a) g é uma função quadrática, com duas raízes reais distintas, sendo uma delas igual a -3.
b) A imagem de g é o intervalo [9, ?).
c) g é bijetora, portanto possui inversa.
d) O domínio de g é o conjunto {xeIR/x?0}
e) g é uma função linear com coeficiente angular negativo.
A resposta correta é a letra C, mas gostaria de saber porque as outras alternativas estão erradas.
Obrigada!


 para todos os pontos x de seu domínio.
para todos os pontos x de seu domínio.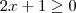 . Isso significa que
. Isso significa que 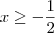 .
.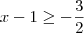 . Disso tiramos que o domínio da função g deve ser
. Disso tiramos que o domínio da função g deve ser 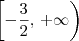 .
. , temos que
, temos que 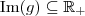 .
.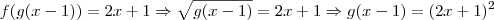 .
.![g(u) = [2(u + 1)+1]^2 \Rightarrow g(u) = (2u + 3)^2 g(u) = [2(u + 1)+1]^2 \Rightarrow g(u) = (2u + 3)^2](/latexrender/pictures/894862fd8852b5846716758af4729a35.png) .
.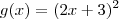 .
. .
.![\left[\sqrt{g(x-1)}\right]^2 = g(x-1) \left[\sqrt{g(x-1)}\right]^2 = g(x-1)](/latexrender/pictures/627cb3375552d83f515ee7ac641816b7.png) , pois sabíamos que g(x-1) é um número positivo.
, pois sabíamos que g(x-1) é um número positivo.![\left[\sqrt{g(x-1)}\right]^2 = |g(x-1)| \left[\sqrt{g(x-1)}\right]^2 = |g(x-1)|](/latexrender/pictures/6fbbe4bb4cb8a3a34e39a92c1477b5da.png) .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
