 por Pre-Universitario » Sex Ago 05, 2011 18:09
por Pre-Universitario » Sex Ago 05, 2011 18:09
Num trabalho pratico de topografia, um engenheiro civil deve determinar
altura de um predio situado em terreno plano. Instalado o aparelho adequado num ponto do terreno,
o topo do predio é visto sob um angulo de 60 Graus.
Afastando-se o aparelho mais 10 metros do edificio, seu topo passa a ser visto sob um angulo de 45 Graus.
Desprezando a altura do aparelho, calcule a altura do predio?
Bom ! Fiz desta forma:
![tg 60 = c.o./c.a. \Rightarrow \sqrt[]{3} = h/a
\Rightarrow h = \sqrt[]{3}a
tg 45 = c.o./c.a. \Rightarrow 1 = h/10+a \Rightarrow h = 1(10+a)
\Rightarrow \sqrt[]{3} = 10+1a \Rightarrow \sqrt[]{3} -1a = 10
\Rightarrow a = 10/\sqrt[]{3}-1. tg 60 = c.o./c.a. \Rightarrow \sqrt[]{3} = h/a
\Rightarrow h = \sqrt[]{3}a
tg 45 = c.o./c.a. \Rightarrow 1 = h/10+a \Rightarrow h = 1(10+a)
\Rightarrow \sqrt[]{3} = 10+1a \Rightarrow \sqrt[]{3} -1a = 10
\Rightarrow a = 10/\sqrt[]{3}-1.](/latexrender/pictures/4b7ed9d8a5932f555acca7135bc4e0f6.png)
Se alguem poder faze-la correta ou ver se esta correta
obg.
Editado pela última vez por
Pre-Universitario em Sex Ago 05, 2011 18:38, em um total de 1 vez.
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por Pre-Universitario » Sex Ago 05, 2011 18:19
por Pre-Universitario » Sex Ago 05, 2011 18:19
Pre-Universitario escreveu:Num trabalho pratico de topografia, um engenheiro civil deve determinar
altura de um predio situado em terreno plano. Instalado o aparelho adequado num ponto do terreno,
o topo do predio é visto sob um angulo de 60 Graus.
Afastando-se o aparelho mais 10 metros do edificio, seu topo passa a ser visto sob um angulo de 45 Graus.
Desprezando a altura do aparelho, calcule a altura do predio?
Bom ! Fiz desta forma:
![tg 60 = c.o./c.a. \Rightarrow \sqrt[]{3} = h/a
\Rightarrow h = \sqrt[]{3}a
tg 45 = c.o./c.a. \Rightarrow 1 = h/10+a \Rightarrow h = 1(10+a)
\Rightarrow \sqrt[]{3} = 10+1a \Rightarrow \sqrt[]{3} -1a = 10
\Rightarrow a = 10/\sqrt[]{3}-1. tg 60 = c.o./c.a. \Rightarrow \sqrt[]{3} = h/a
\Rightarrow h = \sqrt[]{3}a
tg 45 = c.o./c.a. \Rightarrow 1 = h/10+a \Rightarrow h = 1(10+a)
\Rightarrow \sqrt[]{3} = 10+1a \Rightarrow \sqrt[]{3} -1a = 10
\Rightarrow a = 10/\sqrt[]{3}-1.](/latexrender/pictures/4b7ed9d8a5932f555acca7135bc4e0f6.png)
Se alguem poder faze-la correta ou ver se esta correta
obg.
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por ant_dii » Sex Ago 05, 2011 18:37
por ant_dii » Sex Ago 05, 2011 18:37
A primeira parte beleza, sendo

a altura do edifício e

a distância do aparelho até o edifício:
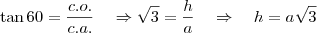
Já que ele andou dez metros mais longe do prédio (?:dúvida aqui, mais longe do prédio ou mais perto?):

Então, por fim, substituindo h vem:
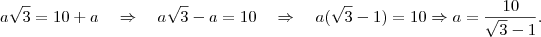
E

que é aproximadamente 24 metros de altura.
Estava certo, mas cuidado com os parenteses. Até mais

Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Pre-Universitario » Sex Ago 05, 2011 18:43
por Pre-Universitario » Sex Ago 05, 2011 18:43
bom brother, na questao, afirma que o engenheiro afastou o apararelho 10 metros
Editado pela última vez por
Pre-Universitario em Sex Ago 05, 2011 18:56, em um total de 1 vez.
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por Pre-Universitario » Sex Ago 05, 2011 18:52
por Pre-Universitario » Sex Ago 05, 2011 18:52
pode me explicar como xegou a conclusão de 24m
a questao no livro pede como fração mesmo
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por ant_dii » Sex Ago 05, 2011 19:08
por ant_dii » Sex Ago 05, 2011 19:08
Pre-Universitario escreveu:pode me explicar como xegou a conclusão de 24m
a questao no livro pede como fração mesmo
Então fica,
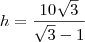
.
Você tem a resposta da questão??
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Pre-Universitario » Sex Ago 05, 2011 19:09
por Pre-Universitario » Sex Ago 05, 2011 19:09
valeu depois deixo mas questoes ai pra quem qser me ajudar
valeu e seja um bom professor
fui !!
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quero saber se minha resposta está correta
por Raquel299 » Seg Mar 09, 2015 09:53
- 3 Respostas
- 2741 Exibições
- Última mensagem por Raquel299

Sex Abr 10, 2015 10:49
Funções
-
- Esta minha resolucao está correta?
por SsEstevesS » Dom Nov 27, 2011 10:29
- 0 Respostas
- 2968 Exibições
- Última mensagem por SsEstevesS

Dom Nov 27, 2011 10:29
Geometria Plana
-
- Re: Derivada - Resposta correta?
por iceman » Dom Set 16, 2012 22:22
- 1 Respostas
- 1507 Exibições
- Última mensagem por MarceloFantini

Dom Set 16, 2012 22:27
Cálculo: Limites, Derivadas e Integrais
-
- Integrais feita, esta correta?
por Maykids » Qua Jun 22, 2011 13:50
- 4 Respostas
- 2837 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 24, 2011 00:19
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Está correta a resolução?
por Fabio Wanderley » Qui Nov 29, 2012 11:47
- 4 Respostas
- 3773 Exibições
- Última mensagem por Fabio Wanderley

Sex Nov 30, 2012 09:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![tg 60 = c.o./c.a. \Rightarrow \sqrt[]{3} = h/a
\Rightarrow h = \sqrt[]{3}a
tg 45 = c.o./c.a. \Rightarrow 1 = h/10+a \Rightarrow h = 1(10+a)
\Rightarrow \sqrt[]{3} = 10+1a \Rightarrow \sqrt[]{3} -1a = 10
\Rightarrow a = 10/\sqrt[]{3}-1. tg 60 = c.o./c.a. \Rightarrow \sqrt[]{3} = h/a
\Rightarrow h = \sqrt[]{3}a
tg 45 = c.o./c.a. \Rightarrow 1 = h/10+a \Rightarrow h = 1(10+a)
\Rightarrow \sqrt[]{3} = 10+1a \Rightarrow \sqrt[]{3} -1a = 10
\Rightarrow a = 10/\sqrt[]{3}-1.](/latexrender/pictures/4b7ed9d8a5932f555acca7135bc4e0f6.png)


 a altura do edifício e
a altura do edifício e  a distância do aparelho até o edifício:
a distância do aparelho até o edifício: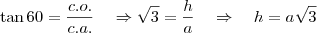

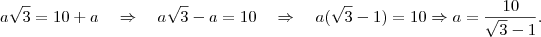
 que é aproximadamente 24 metros de altura.
que é aproximadamente 24 metros de altura.

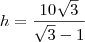 .
.




