É o seguinte, entendi a representação geométrica do quadrado da diferença de dois termos. Agora estou tentando entender a representaçao geométrica da diferença de dois termos.
Fiz o desenho de um quadrado, para tentar explicar a minha duvida a respeito da representaçao geométrica.
Entendi que no quadrado da soma de dois termos, para calcular a area do quadrado maior, você tem que elevar o lado desse quadrado maior ao quadrado. Também tem como achar a aréa do quadrado maior, somando as áreas dos dois quadrados menores, + as areas dos dois retangulos.
Agora estou tentando entender geometricamente
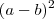
A explicação para
 é de que pegando a área do quadrado grande, menos as duas areas dos retângulos, ficarei somente com a área do quadrado amarelo e do quadrado verde né? ou estou entendendo errado?
é de que pegando a área do quadrado grande, menos as duas areas dos retângulos, ficarei somente com a área do quadrado amarelo e do quadrado verde né? ou estou entendendo errado?Obrigado





 , avisa que eu resolvo.
, avisa que eu resolvo.

