 por m0x0 » Sáb Jul 23, 2011 20:18
por m0x0 » Sáb Jul 23, 2011 20:18
Boas a todos,
Ando a estudar para Teoria dos Anéis e surgiu-me uma dúvida de uma demonstração:
Teorema: se R é Anel comutativo com 1 no qual valem as Leis do Cancelamento, então R é Domínio de Integridade.
DEM:
Sendo R um Domínio de Integridade;


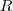

;
Tal que:

então:
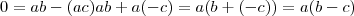
e como a é diferente de 0 =>
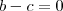
, ou seja,

O que eu não entendo é o facto de dizerem:
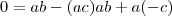
Se alguém me puder explicar o porquê desta igualdade, ficarei muito agradecido, penso que seja pela unicidade do oposto, mas não entendo a lógica disto!! :|
m0x0
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Corrijam] Todo Corpo é domínio de Integridade
por juliomarcos » Dom Set 14, 2008 00:46
- 4 Respostas
- 8518 Exibições
- Última mensagem por juliomarcos

Qua Set 24, 2008 01:03
Álgebra Elementar
-
- Cancelamento em cadeia
por Jhenrique » Qua Out 31, 2012 02:25
- 2 Respostas
- 1961 Exibições
- Última mensagem por Jhenrique

Qua Out 31, 2012 18:18
Álgebra Elementar
-
- lei do cancelamento universal do estudante
por admin » Qua Set 10, 2008 18:19
- 1 Respostas
- 5325 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 19:51
Piadas
-
- Dominios e Contradominios
por joaofonseca » Sáb Out 01, 2011 15:09
- 8 Respostas
- 6837 Exibições
- Última mensagem por MarceloFantini

Ter Out 04, 2011 21:19
Funções
-
- Domínios de uma função
por ah001334 » Seg Nov 07, 2011 14:08
- 20 Respostas
- 12717 Exibições
- Última mensagem por procyon

Seg Nov 07, 2011 22:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


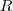
 ;
; então:
então: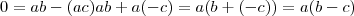 e como a é diferente de 0 =>
e como a é diferente de 0 => 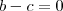 , ou seja,
, ou seja, 
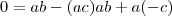


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.