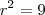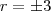por reyerak » Qui Jul 21, 2011 19:26
por reyerak » Qui Jul 21, 2011 19:26
Determine o(s) valor(es) que "r" deve assumir para que o ponto (r,2) diste cinco unidades do ponto (0,-2).
Resposta:


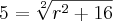

Dps disso não sei o que fazer, to batendo minha cabeça mais não lembro de jeito nenhum, ja fiz o resto do meu trabalho de recuperação,porem esse exercicio ta me atormentando.
obrigado pela atenção.
ops, postei na area errada, se algum adm puder mudar agradeço. desculpe
-

reyerak
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jul 21, 2011 18:46
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica
- Andamento: cursando
 por Molina » Qui Jul 21, 2011 19:53
por Molina » Qui Jul 21, 2011 19:53
Boa noite.
Você estava indo bem, mas deve ter esquecido desta propriedade:
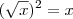
Ou seja, continue sua conta e "corte" a raiz com a potência dois. Continue a conta e ache o valor de r.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por reyerak » Qui Jul 21, 2011 20:02
por reyerak » Qui Jul 21, 2011 20:02
Nossa muito obrigado, consegui resolver era isso mesmo que eu estava esquecendo.
Obrigado

-

reyerak
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jul 21, 2011 18:46
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica
- Andamento: cursando
 por reyerak » Qui Jul 21, 2011 20:36
por reyerak » Qui Jul 21, 2011 20:36
Surgiu uma nova duvida,
no enunciado tem alternativas...
a) r= 3 e r= -3
b) r= -11
c) r= -11 e r= 11
d) r= 3
e) r= +-
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
estou na duvida se a resposta é A ou D
Eu fiz isso:

obrigado pela atenção.
-

reyerak
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jul 21, 2011 18:46
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica
- Andamento: cursando
 por m0x0 » Qui Jul 21, 2011 20:43
por m0x0 » Qui Jul 21, 2011 20:43
Essa não podes fazer da raíz quadrada de -9 porque vai-te dar impossível, pelo menos nos números reais claro, mas se fores para os números complexos já consegues - nos números complexos a raízquadrada(-1)=i mas não entremos por aí!

Mas a solução está em:
![r=\sqrt[2]{9}=3 \cup r=\sqrt[2]{9}=-3 r=\sqrt[2]{9}=3 \cup r=\sqrt[2]{9}=-3](/latexrender/pictures/e19bde04e1f2c2a29978894539d621d9.png)
são as tuas soluções.
Editado pela última vez por
m0x0 em Qui Jul 21, 2011 20:48, em um total de 1 vez.
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Qui Jul 21, 2011 20:47
por Molina » Qui Jul 21, 2011 20:47
Boa noite.
Você não pode fazer aquilo que questionou.
Perceba que você trocou de lado o
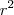
e não mudou o sinal dele.
O certo é você ficar com
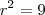
Com isso, temos que:
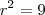

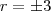

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por reyerak » Qui Jul 21, 2011 20:50
por reyerak » Qui Jul 21, 2011 20:50
Obrigado novamente, estava com duvida nisso e não posso errar nada desse trabalho de recuperação pq minha situação em matematica ta ruim.
agradeço me ajudo e esclareceu minhas duvidas.
-

reyerak
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jul 21, 2011 18:46
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informatica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- distancia entre dois pontos
por belinha26 » Sex Jul 05, 2013 22:26
- 0 Respostas
- 1565 Exibições
- Última mensagem por belinha26

Sex Jul 05, 2013 22:26
Álgebra Linear
-
- Calculo Distancia Entre dois pontos
por AndyPere » Seg Abr 05, 2010 12:22
- 0 Respostas
- 3186 Exibições
- Última mensagem por AndyPere

Seg Abr 05, 2010 12:22
Desafios Médios
-
- DÚVIDA EXERCÍCIO Distância entre pontos
por Danilo » Seg Abr 16, 2012 02:39
- 6 Respostas
- 9257 Exibições
- Última mensagem por LuizAquino

Ter Abr 17, 2012 11:23
Geometria Analítica
-
- Distância entre pontos no ciclo trigonométrico.
 por Sobreira » Dom Nov 18, 2012 17:44
por Sobreira » Dom Nov 18, 2012 17:44
- 4 Respostas
- 4237 Exibições
- Última mensagem por Sobreira

Dom Nov 18, 2012 23:59
Trigonometria
-
- [distancia entre pontos e planos] DUVIDA
por Erickvilela » Qui Fev 14, 2013 21:38
- 2 Respostas
- 2236 Exibições
- Última mensagem por e8group

Sex Fev 15, 2013 08:59
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


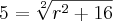



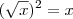



![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)

![r=\sqrt[2]{9}=3 \cup r=\sqrt[2]{9}=-3 r=\sqrt[2]{9}=3 \cup r=\sqrt[2]{9}=-3](/latexrender/pictures/e19bde04e1f2c2a29978894539d621d9.png) são as tuas soluções.
são as tuas soluções.
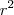 e não mudou o sinal dele.
e não mudou o sinal dele.