 por OtavioBonassi » Sáb Jul 16, 2011 14:54
por OtavioBonassi » Sáb Jul 16, 2011 14:54
Fala galera, sei que esse é um problema mais de derivada ,mas resolvi postar aqui pra se alguem tiver algum outro tipo de resolução .
O enunciado é o seguinte "Quantos pontos de inflexão tem a função f
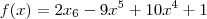
?"
Eu resolvi o problema mas o número de inflexoes deu 3, mas o gabarito diz que tem 2 pontos de inflexão apenas. Aonde esta o caô ?
Valeu !
p.s. esse primeiro termo é x elevado a 6, nao sei qual o problema de formatação da fórmula.
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por LuizAquino » Sáb Jul 16, 2011 18:04
por LuizAquino » Sáb Jul 16, 2011 18:04
OtavioBonassi escreveu:Eu resolvi o problema mas o número de inflexoes deu 3, mas o gabarito diz que tem 2 pontos de inflexão apenas. Aonde esta o caô ?
São de fato 2 pontos de inflexão. Envie a sua resolução para que possamos identificar onde você está errando.
OtavioBonassi escreveu:p.s. esse primeiro termo é x elevado a 6, nao sei qual o problema de formatação da fórmula.
Perceba que dentro do ambiente LaTeX você digitou
- Código: Selecionar todos
x_6
ao invés de
- Código: Selecionar todos
x^6
O primeiro comando tem como resultado
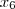
, mas o segundo tem como resultado
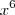
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] Concavidade e pontos de Inflexão
por fabriel » Sex Set 21, 2012 22:56
- 3 Respostas
- 2439 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 01:18
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar pontos de inflexão
por alienpuke » Qui Nov 12, 2015 11:31
- 2 Respostas
- 3765 Exibições
- Última mensagem por alienpuke

Ter Nov 17, 2015 10:01
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: Achar os extremos da função(min/máx/inflexão)
por Fernandobertolaccini » Dom Jul 13, 2014 22:50
- 1 Respostas
- 1781 Exibições
- Última mensagem por e8group

Seg Jul 14, 2014 01:48
Cálculo: Limites, Derivadas e Integrais
-
- função e conjunto de pontos
por Andreza » Sáb Nov 12, 2011 10:07
- 1 Respostas
- 1329 Exibições
- Última mensagem por nietzsche

Sáb Nov 12, 2011 15:21
Funções
-
- Função de duas variavéis nos pontos (x,y).
por Sobreira » Qui Abr 11, 2013 08:55
- 1 Respostas
- 1969 Exibições
- Última mensagem por marinalcd

Sex Abr 12, 2013 15:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
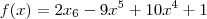 ?"
?"

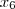 , mas o segundo tem como resultado
, mas o segundo tem como resultado 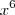 .
.