 por Claudin » Qui Jul 14, 2011 21:16
por Claudin » Qui Jul 14, 2011 21:16
No vídeo do colaborador Luiz Aquino
-->
http://www.youtube.com/watch?v=-TNbOIad ... ideo_titleNo exemplo 3 em 6:18
Não intendi como derivar o numerador e o denominador
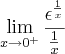
Sendo mais direto, não compreendi o aparecimento do
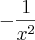
no numerador.
E também não compreendi o porque de ser um valor negativo no denominador, não seria positivo ao derivar?
Gostaria de ter uma explicação detalhada sobre as derivadas que obtive neste exercício.
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jul 14, 2011 22:10
por LuizAquino » Qui Jul 14, 2011 22:10
DicasNote que
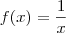
é o mesmo que

. Agora, aplique a regra para derivar funções do tipo

.
Além disso, note que para derivar a função

é necessário usar a Regra da Cadeia.
Fazendo

e
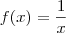
, temos que

. Portanto,
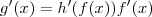
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sex Jul 15, 2011 15:01
por Claudin » Sex Jul 15, 2011 15:01
Na maioria das vezes eu confundo

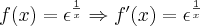
Em ambas utilizo a regra da cadeia?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jul 15, 2011 16:05
por LuizAquino » Sex Jul 15, 2011 16:05
Claudin escreveu:Na maioria das vezes eu confundo

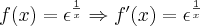
Em ambas utilizo a regra da cadeia?
Só é necessário utilizar apenas no segundo caso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Jul 15, 2011 20:08
por MarceloFantini » Sex Jul 15, 2011 20:08
A regra da cadeia no primeiro caso resulta em 1, portanto não faz diferença.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Jul 15, 2011 20:27
por LuizAquino » Sex Jul 15, 2011 20:27
MarceloFantini escreveu:A regra da cadeia no primeiro caso resulta em 1, portanto não faz diferença.
Por isso que eu disse que só é
necessário utilizar apenas no segundo caso. No primeiro caso não é
necessário utilizar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Jul 15, 2011 20:30
por MarceloFantini » Sex Jul 15, 2011 20:30
Eu sei disso, foi para o Claudin.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Jul 15, 2011 20:57
por LuizAquino » Sex Jul 15, 2011 20:57
MarceloFantini escreveu:Eu sei disso, foi para o Claudin.
Ok!

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Jul 16, 2011 00:35
por Claudin » Sáb Jul 16, 2011 00:35
Correto, eu tinha efetuado a regra da cadeia em ambos e percebi que o resultado foi 1 por isso não fez diferença.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Jul 16, 2011 15:20
por MarceloFantini » Sáb Jul 16, 2011 15:20
Em ambos não, note que

, portanto a regra da cadeia é 1 apenas no primeiro caso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1918 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- regra de L' Hospital
por matmatco » Qua Nov 30, 2011 13:47
- 5 Respostas
- 2479 Exibições
- Última mensagem por matmatco

Sáb Dez 03, 2011 07:10
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'hospital
 por samra » Dom Ago 19, 2012 18:37
por samra » Dom Ago 19, 2012 18:37
- 1 Respostas
- 2433 Exibições
- Última mensagem por e8group

Dom Ago 19, 2012 19:58
Cálculo: Limites, Derivadas e Integrais
-
- Derivada regra de L'Hospital
por Wumaxeb » Sex Mai 27, 2011 22:19
- 2 Respostas
- 3108 Exibições
- Última mensagem por Molina

Sex Mai 27, 2011 23:24
Cálculo: Limites, Derivadas e Integrais
-
- [Regra de L'Hospital] Indeterminções
por erickm93 » Seg Jun 24, 2013 11:47
- 1 Respostas
- 1649 Exibições
- Última mensagem por Man Utd

Qui Jun 27, 2013 11:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
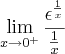
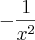 no numerador.
no numerador.

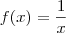 é o mesmo que
é o mesmo que  . Agora, aplique a regra para derivar funções do tipo
. Agora, aplique a regra para derivar funções do tipo  .
. é necessário usar a Regra da Cadeia.
é necessário usar a Regra da Cadeia. e
e  . Portanto,
. Portanto, 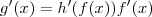 .
.

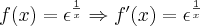

 , portanto a regra da cadeia é 1 apenas no primeiro caso.
, portanto a regra da cadeia é 1 apenas no primeiro caso.

 , avisa que eu resolvo.
, avisa que eu resolvo.

