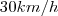 faz um percurso em duas horas. Se a velocidade
faz um percurso em duas horas. Se a velocidadedobrar, em quanto tempo ele fará o percurso?
Bom, pelo que eu tentei, se resolve com regra de três.
Se ouver outra maneira, me digam, por favor.
Velocidade (km/h) -------- Tempo (h's)
30 km ------------------------- 2h
60 km ------------------------- x
Como a Grandeza é inversamente proporcional, pelo fato de que, quanto maior a velocidade menor é o tempo.
R: No gabarito diz 1h. só que, eu consegui achar 4h, e agora?
Abraço


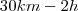
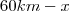
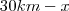
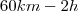

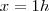


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)