Boa tarde, Dimas e Gustavo.
Há dois caminhos para resolver este problema: o primeiro é fazer um esboço do gráfico, dando alguns valores para x e vendo como a tangente se comporta. Assim você encontrará as resposta que precisa.
O outro procedimento é resolver usando algumas definições já conhecidas da função tangente:
Domínio:

Na desigualdade a cima, ao invés de x você vai colocar o que há dentro do parênteses da função tangente que você está trabalhando. e resolver a desiguldade, isolando x.
Imagem: Toda função tangente tem imagem Real (R).
Período: Período da tangente:

.
Para as próximas questões, tente deixar claro quais são as suas dúvidas e suas tentativas, ok?

 são, respectivamente:
são, respectivamente:
 R /
R / 




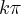 , k
, k  R }, R e
R }, R e 

 R / x
R / x 


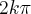 , k
, k  R }, R e 2
R }, R e 2

 R /
R / 


 }, R e
}, R e 

 R /
R / 


 }, R e 2
}, R e 2







 indica que ele continua indo na direção negativa (sentido horário).
indica que ele continua indo na direção negativa (sentido horário).
 .
.



