Tem um exercício aqui que pede para achar a equação da metade inferior da circunferência
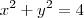 . Bom, pela equação dá pra notar que a circunferência tem centro na origem e raio 2, certo? Então. A metade inferior da circunferência vai ser onde
. Bom, pela equação dá pra notar que a circunferência tem centro na origem e raio 2, certo? Então. A metade inferior da circunferência vai ser onde  . Acontece que isolando
. Acontece que isolando  a equação fica
a equação fica ![y = \sqrt[2]{4 - x^2} y = \sqrt[2]{4 - x^2}](/latexrender/pictures/fffd97884b21f424a3def652a542ed99.png) . Meus limitados conhecimentos matemáticos me dizem que não é possível o resultado de uma raiz com índice par ser um número real negativo. Nesse caso eu tenho que usar números complexos? Aliás, existe lei de função com números complexos? o.O'
. Meus limitados conhecimentos matemáticos me dizem que não é possível o resultado de uma raiz com índice par ser um número real negativo. Nesse caso eu tenho que usar números complexos? Aliás, existe lei de função com números complexos? o.O'Tem outro exercício parecido pendindo pra encontrar a equação da metade inferior da parábola
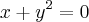 . Também usei o mesmo raciocínio da outra questão e a dúvida é a mesma: existe essa equação?
. Também usei o mesmo raciocínio da outra questão e a dúvida é a mesma: existe essa equação?Vou postar um mooonte de dúvidas ainda, quem puder ir me ajudando eu agradeço MUITOOO!!
Beijos!!


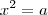 tem solução
tem solução 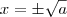 .
.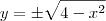 .
.
 Se eu errar uma questão de cálculo por causa disso eu choro uma semana... ¬¬'''''''''
Se eu errar uma questão de cálculo por causa disso eu choro uma semana... ¬¬'''''''''![x = \sqrt[2]{-x} x = \sqrt[2]{-x}](/latexrender/pictures/36c7e130f514d7b885dcead8a7bab4b5.png) . Isso não existe, existe? Meus conhecimentos
. Isso não existe, existe? Meus conhecimentos 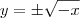 . Essa solução é real
. Essa solução é real 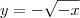 , com
, com  .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

