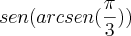
pra min o resultado disse vai ser Sen(60º)
so que eu recebi errado por ela , porque eu so expliquei que o arcsen é a inversa de seno, logo
arcsen de pi/3 sera o angulo de 60º
o que esta errado e como que eu resolvo essa questão?
desde ja agredeço

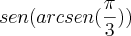

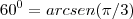
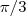 radianos, é o mesmo que 60 graus.
radianos, é o mesmo que 60 graus.
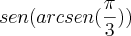
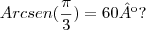
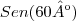


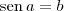 , então
, então 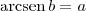 .
.
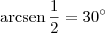
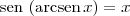 , para todo x no domínio do arcoseno.
, para todo x no domínio do arcoseno.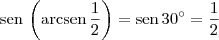
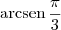 e temos que
e temos que 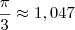 (note como nesse caso devemos enxergar
(note como nesse caso devemos enxergar  como um número e não como um ângulo).
como um número e não como um ângulo).Maykids escreveu:(...)
(...)
esse A ai entrou sozinho no editor, desconcidere.
[tex]60^\circ[/tex]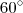


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes

 .
.



