 por -civil- » Qui Jul 07, 2011 23:19
por -civil- » Qui Jul 07, 2011 23:19
Suponha que
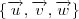
seja L.I.. dado
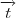
, existem

tais que

. Prove que, se
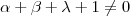
, então

-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sex Jul 08, 2011 10:55
por LuizAquino » Sex Jul 08, 2011 10:55
Reveja o texto do exercício, pois está faltando informação. Está faltando, por exemplo, algo como: "(...) então
 é ...
é ...".
Por favor, transcreva o texto
exatamente como aparece no exercício original.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DEpendência Linear] Álgebra Linear
por Ronaldobb » Ter Mar 25, 2014 14:22
- 1 Respostas
- 1113 Exibições
- Última mensagem por young_jedi

Qui Mar 27, 2014 00:10
Álgebra Linear
-
- [GA] Dependência Linear
por Larissa28 » Ter Mar 31, 2015 20:31
- 4 Respostas
- 1771 Exibições
- Última mensagem por Larissa28

Qua Abr 01, 2015 20:19
Geometria Analítica
-
- Dependência e independência linear
por MtHenrique » Dom Mai 04, 2014 11:38
- 3 Respostas
- 2683 Exibições
- Última mensagem por e8group

Dom Mai 04, 2014 22:43
Álgebra Linear
-
- [Dependência linear] Sequência de 3
por ViniciusAlmeida » Sáb Mar 21, 2015 09:32
- 0 Respostas
- 952 Exibições
- Última mensagem por ViniciusAlmeida

Sáb Mar 21, 2015 09:32
Geometria Analítica
-
- [Dependência linear] Provar
por ViniciusAlmeida » Ter Mar 24, 2015 08:54
- 1 Respostas
- 3239 Exibições
- Última mensagem por adauto martins

Qua Mar 25, 2015 15:26
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
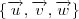 seja L.I.. dado
seja L.I.. dado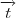 , existem
, existem  tais que
tais que  . Prove que, se
. Prove que, se 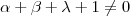 , então
, então 

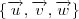 seja L.I.. dado
seja L.I.. dado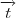 , existem
, existem  tais que
tais que  . Prove que, se
. Prove que, se 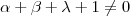 , então
, então 

 é ...".
é ...".