Relacione os elementos e os conjuntos dados utilizando os simbolos E ou E cortado
a)3 N* b) -5 N* C) fração de 8 e 4 Z d) 0,18 Z e) raiz de -4 Q f) -0,3 R g) - raiz de 5 Z h)fração de 5 e 10 N


 (pertence) e
(pertence) e  (não pertence). Eles são usados para simbolizar se um número está em um determinado conjunto ou não.
(não pertence). Eles são usados para simbolizar se um número está em um determinado conjunto ou não.
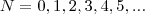
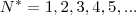

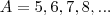
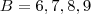

 . O que você quer é achar os valores de x que a parte da esquerda seja igual a zero. Você pode usar a
. O que você quer é achar os valores de x que a parte da esquerda seja igual a zero. Você pode usar a 

 .
.



